座屈解析機能#

1. はじめに#

座屈とは、構造物に荷重を加えたときに、材料の降伏よりも低いレベルで大きく変形してしまう現象です。特に細長い形状や薄い板形状では、座屈が発生しやすいです。このような構造物では材料の降伏強度のほかにも座屈の発生を考慮する必要があります。

CAE での座屈の解析には、大きく分けて線形座屈解析と非線形座屈解析の2種類があります。線形座屈解析とは、座屈前の変位量が小さく、応力、ひずみ値などが荷重に比例すると仮定した条件での座屈解析のことです。Advance/FrontSTR v6.3では線形座屈解析機能を実装しました。

2. 線形座屈解析機能紹介#

2.1. 理論式#

数学的には、座屈がおきるときは、構造物の剛性が特異になります。ここでの線形座屈解析は、臨界座屈係数と、関連した座屈モード形状を求める固有値問題を解きます。そのため、線形座屈解析は座屈固有値解析とも呼ばれます。

構造物の全体剛性マトリクスは一般的に以下の式で表すことができます。

$K =K_L + K_G 　…(1)$

ここで $K_L$ と $K_G$ はそれぞれ線形剛性マトリクスと幾何学剛性マトリクスと表しています。線形座屈解析では、幾何学剛性マトリクスは外力 $q_0$ と比例すると仮定します、すなわち

$K_G(λq_0) = λK_G(q_0)　…(2)$

そのため、線形座屈解析は下記の特異値問題を解くことになります。

$(K_L+λK_G(q_0))x = 0　…(3)$

その非零解が存在する条件は

$p(λ) = |K-λK_G| = 0　…(4)$

となり、固有値問題に帰着します。

3. 座屈解析の事例#

3.1. 梁の座屈解析#

梁要素で様々な支持条件下の座屈解析を実施し、解析結果出力の座屈荷重を理論値と比較しました。

3.1.1. 解析条件#

主な解析条件を表1 に、解析ケースと支持条件を表2に示します。梁には一様な圧縮荷重を負荷しました。

表 1　解析条件

項目	値
梁要素の種類	EULER梁
ヤング率	$E = 7.1×10^{10}[Pa]$
断面積	$A = 1.257×10^{-3}[m^2]$
断面2次モーメント	$I = 1.26×10^{-7}[m^4]$
長さ	$L = 10[m]$
要素分割	$10$ 分割
基準荷重	$1000 [N]$

表 2　解析ケースと支持条件

解析ケース	端点1	端点2	式(5)のn
case1	完全拘束	完全拘束	4
case2	完全拘束	ピン支持	2.046
case3	ピン支持	ピン支持	1

3.1.2. 解析結果#

軸方向に圧縮荷重を受けるオイラーの式における座屈荷重は式(5) で与えられます。n は支持条件によって決まる定数です。

$P = \frac{nπ^2EI}{L^2}　…(5)$

数値解析で得られた座屈荷重をオイラーの座屈荷重を比較した値を表3 に示します。

理論値と解析結果により導出した座屈荷重はよく一致しました。

また図1 に示す座屈変形図の出力により各解析ケースにおける座屈変形モード形状が確認できました。

表 3　座屈荷重の比較

解析ケース	理論値[N]	解析結果荷重係数	解析結果座屈荷重[N]
case1	880.6	0.883	882.9
case2	1801.7	1.806	1806.4
case3	3522.3	3.532	3532.5

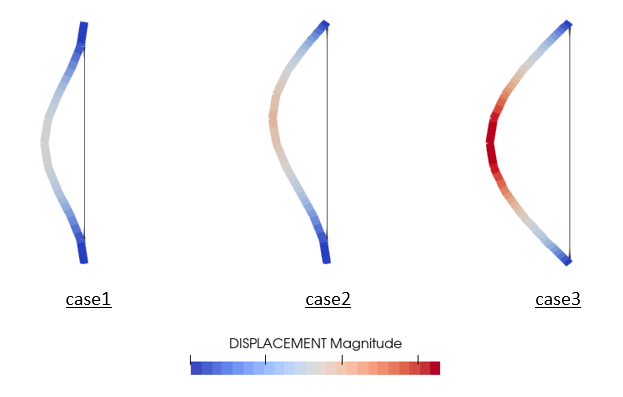
[図1] 変形モード形状

3.2. 薄肉円筒シェルの座屈解析#

薄肉円筒シェルの座屈解析を実施し座屈形状を確認しました。

3.2.1. 解析条件#

解析条件を表4 に示します。モデルの端部は固定端とし、軸方向の圧縮荷重を負荷しました。

表 4　解析条件

項目	値
要素タイプ	四辺形シェル要素
円筒半径	$R = 100 [in]$
板厚	$t = 0.25[in]$
長さ	$L = 400 [in]$
径厚比	$R/t = 400$
ヤング率	$E = 3.0×10^7[lbf/in^2]$
ポアソン比	$ν= 0.3$

3.2.2. 解析結果#

解析結果で得られた座屈荷重を表5 に座屈モード変形図を図2 に示します。

表 5　座屈荷重

出力ﾓｰﾄﾞNo.	円周方向の全波数 n	軸方向の半波数 m	座屈荷重[lbf/in2]
$1$	$10$	$1$	$2.35×10^5$
$13$	$12$	$2$	$3.51×10^5$

[図2] モード1, n=10, m=1

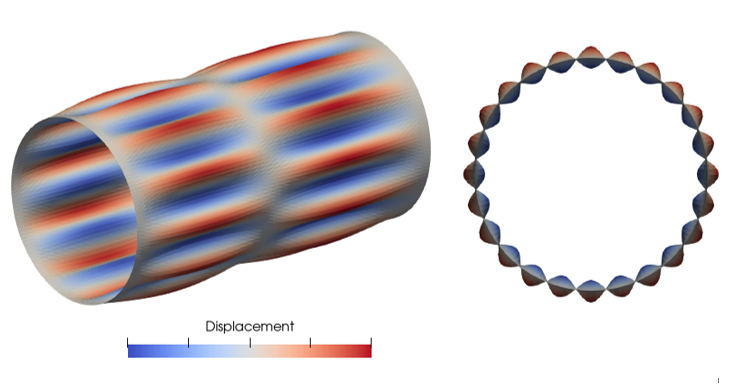
[図3] モード13, n=12, m=2

過去の文献[1][2] などから、概ね R/t が 400 以上では弾性座屈とみなされており、古典的座屈理論値による座屈応力値は式(6) で与えられます。

$σ_{cl}=\frac{1}{√(3(1-ν^2 ) )}・\frac{Et}{R}=0.605 \frac{Et}{R} 　…(6)$

本式から算出される座屈応力値は座屈応力の下限の推定などに利用され、式(6)による算出値は $4.54×10^4 [lbf/in^2]$ であり、解析結果の座屈応力値はそれよりも高い値となりました。

薄肉円筒の座屈応力値は解析モデルの分割数や境界条件などが結果に影響する事が知られていることから数多くの研究がなされ、設計に利用する際には慎重に検討を行う必要があります。

参考文献#

[1] 公益社団法人　土木学会, 座屈設計ガイドライン, 第13章パイプおよびシェル

[2] 松浦真一, 薄肉／厚肉円筒の座屈挙動と設計指針, 圧力技術第37巻第6号, 1999

※ 技術情報誌アドバンスシミュレーションは、アドバンスソフト株式会社ホームページのシミュレーション図書館から、PDFファイル（カラー版）がダウンロードできます。（ダウンロードしていただくには、アドバンス/シミュレーションフォーラム会員登録が必要です。）