GNNサロゲートモデルを用いたジェットエンジンブラケットの解析事例#

概要#

ジェットエンジンブラケットのデータセットを利用し、GNN のサロゲートモデルによる、応力および変位の推定を行う。
グラフニューラルネットワーク（ GNN ）は、グラフデータを基本構造とする特徴量を扱うための手法である。
サロゲートモデルには以下のような事が期待できる。
- FEM と比較した計算速度の向上
- 設計パラメータ変更に対する即時結果確認による対話的設計の実施
- 製品開発期間の短縮・コスト削減など

データセット#

SimJEBデータセット¹#

ジェットエンジンブラケット（ JEB ）のデータセットであるSimJEB（ Whalen et al. 2021 ）を利用
Simulated Jet Engine Bracket Dataset（ SimJEB ）
JEB のデザインコンペに投稿されたCADデータから作成
4 節点 4 面体要素と剛体要素からなるメッシュが提供されている（データ数：380 ）
計算結果も提供されているが、本検討ではメッシュデータのみ借用

データセット作成の流れ#

SimJEB データセットをもとに解析条件やメッシュを調整し、GNN 用のデータセットを作成

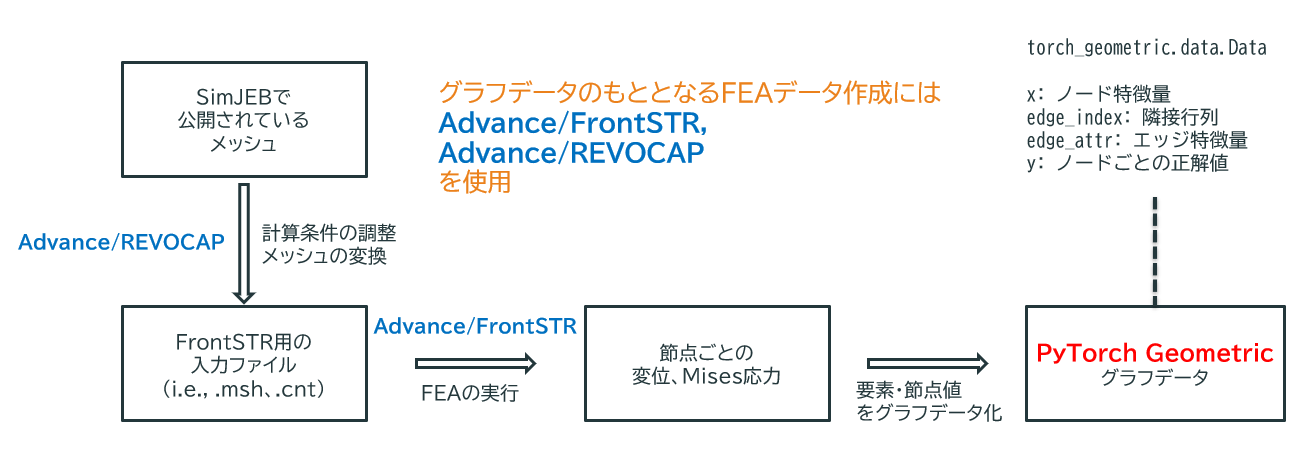
FEA計算条件#

材料：Ti-6Al-4V
- ヤング率： $113.8 GPa$
- ポアソン比： $0.342$
- 密度： $4.470 g/cm^3$
メッシュ規模（統計値）
- 要素タイプ：四面体1次要素
- 節点数の平均値：80,968
- 節点数の標準偏差：40,113.5
- 節点数の最小値：18,141
- 節点数の最大値：219,357

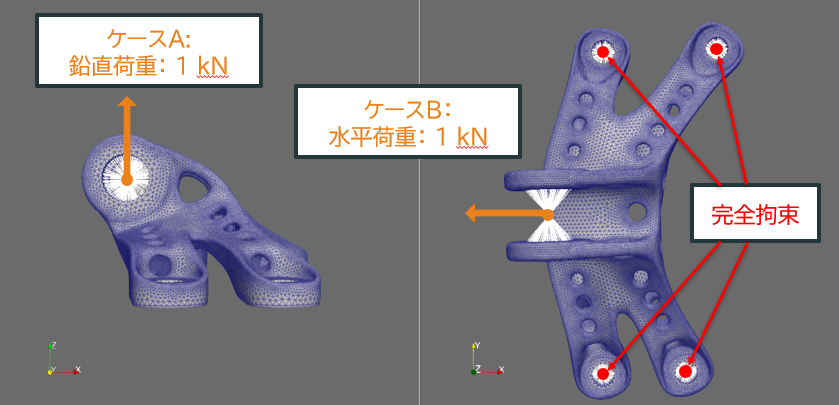
※すべてのデータが同じ条件設定が可能なトポロジーを持つ

グラフデータへの変換#

FEA 用メッシュの節点をノード、要素をエッジとしてグラフデータを作成

同じ要素を構成する節点間にエッジを構成

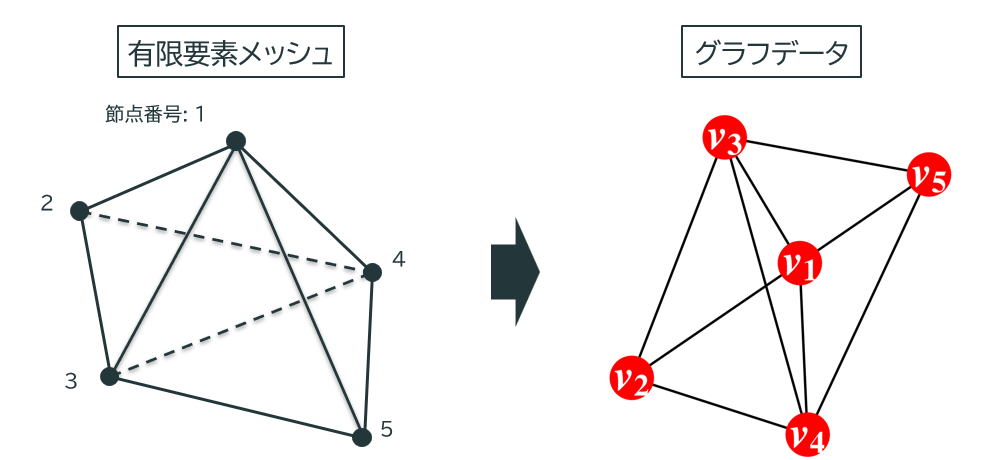
4 節点四面体要素 ×2 の場合

FEA 用メッシュの節点をノード、要素をエッジとしてグラフデータを作成

同じ要素を構成する節点間にエッジを構成

それぞれのノードに対してノード特徴量と正解値、それぞれのエッジに対してエッジ特徴量を与えた

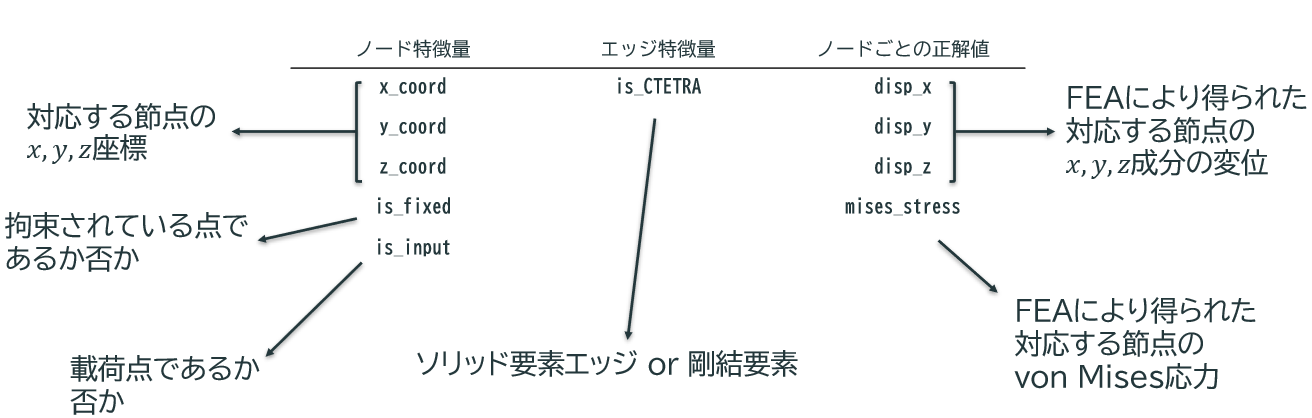
※is_xxxは二値変数

機械学習モデルと学習#

適用した GNN 手法： GCN と GAT#

本検討では、GNN の Message passing の中でも定番とされる GCN および GAT を用いた

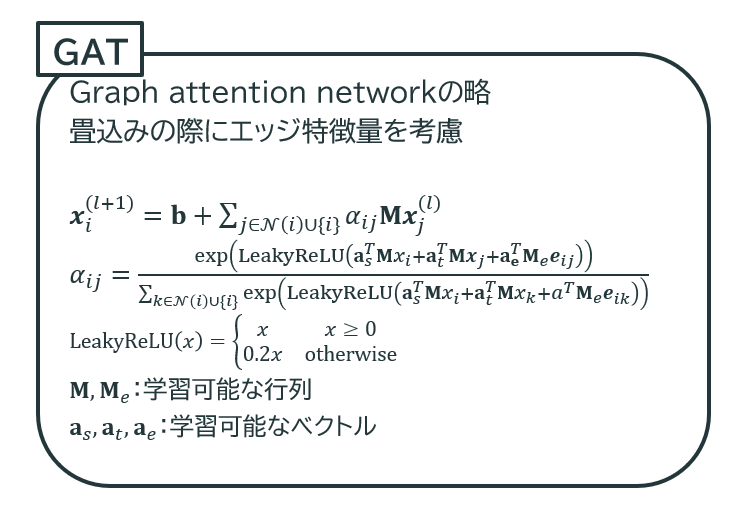
GNNモデル：概要#

モデルは、サイズ、GNN 層後の活性化関数の有無、使用する GNN の種類、予測対象とする変数、載荷方向の 5 つの要素を変更して複数作成した
学習に際しては、オプティマイザを Adam、損失関数を MSE とし、学習率を $1.0 × 10^{-3}$ とした

GNNモデル：詳細#

GNN と線形層 3 層ずつのモデル（ Small ）と、4 層ずつのモデル（ Medium ）を用意

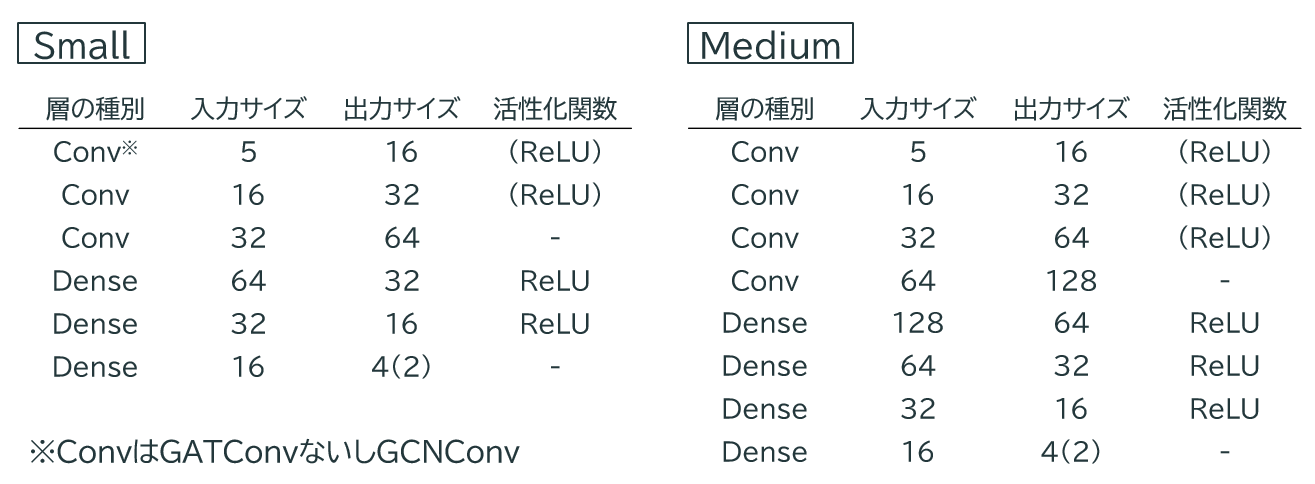
結果#

データセットのFEAの計算時間#

simJEB のデータセット数：380
FEM のモデル規模が大きく学習時にメモリ不足に陥った10ケースを除外
全体のデータセット数：370
80% を学習データセット、20% を評価データセットとした。
計算条件
- 線形静解析
- ソルバー：直接法
- Windows WSL 上で実行
- シリアル計算

計算実行：数時間で終了

※非線形性が加わると計算時間は大幅に増加する

GNN学習に要した計算時間#

計算は WSL2 上の Ubuntu 24.04 LTS 上で実施

CPU : 13th Gen Intel(R) Core(TM) i9-13900　→　8つのPコア、16のEコア

GPU : NVIDIA T1000　→　896 の CUDA コア

RAM : 31.7GB

グラフのサイズが大きく、Medium では GPU のメモリでは容量が不足したため、CPU 上で学習を行った。計算時間はおおよそ次のようになった：

学習に伴う損失関数の推移（鉛直載荷）#

鉛直載荷の場合でモデルサイズと活性化関数についての検討を行った
Small と Medium では僅差ながら Medium が優れるが、SmallRelu と Medium では SmallRelu が優れる
MediumRelu で学習率を $1.0×10^{−3}$ とすれば SmallReluよりも性能が良いことが予想されるが、 Medium は Small の倍以上の計算時間を要するため、SmallRelu を基準として用いることとした
目的変数を変位のみにする場合、MSE は小さくとも変位の推定値精度に顕著な変化はなかった

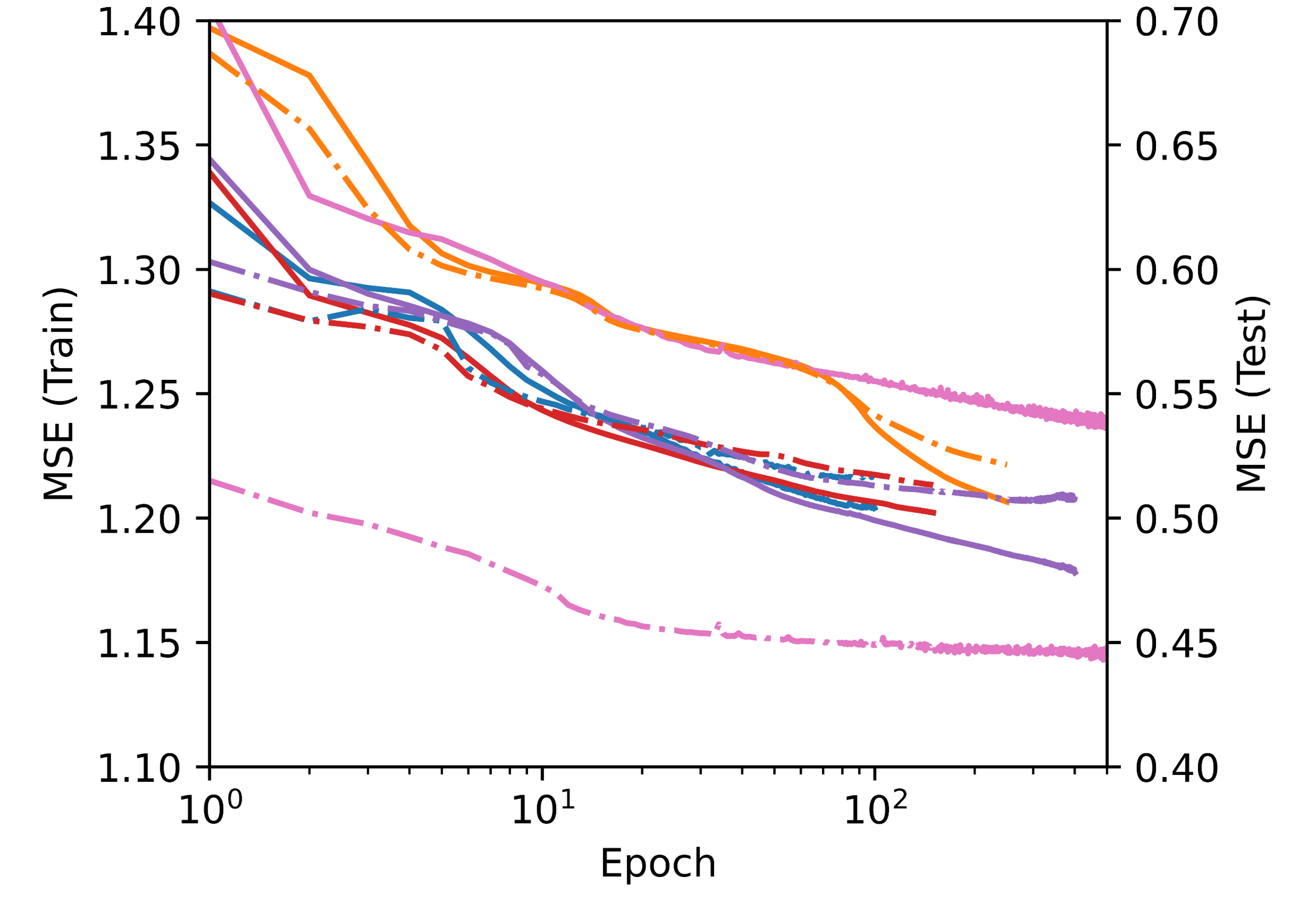
※MediumRelu のみ学習率が1.0×10⁻⁴ すべて GNN 層は GAT

鉛直載荷　予測結果の一例（ $𝒖_𝒙$ ）#

変位の 𝑥 成分の比較

GNN（ GAT、SmallRelu ）による予測値は、傾向と値の双方においてFEAによる結果とおおむね整合
GNN の予測値のほうが一部大きな値を予測している箇所もみられる

鉛直載荷　予測結果の一例（ $𝒖_𝒚$ ）#

変位の 𝑦 成分の比較

GNN（ GAT、SmallRelu ）による予測値は FEA による結果と部分的に整合
右側の脚部では、予測値と正解値で正負が合致しない
- 標準化しているためわからないが、そもそも振幅が小さい
- FEA の結果がメッシュの切り方等に影響されており、物理的な根拠を欠いている可能性も

鉛直載荷　予測結果の一例（ $𝒖_𝒛$ ）#

変位の 𝑧 成分の比較

GNN（ GAT、SmallRelu ）による予測値は、傾向と値の双方において FEA による結果とおおむね整合
𝑢_𝑥 の場合とおおよそ同様の傾向

鉛直載荷　予測結果の一例（Mises応力）#

Mises 応力の比較

変位の 𝑥 成分や 𝑧 成分と異なり、 GNN（ GAT、SmallRelu ）による予測値は FEA によるそれと合致せず
Mises 応力は応力集中箇所で局所的に大きな値をとる　→　ニューラルネットで扱うことが困難
おおまかな応力集中箇所を知る目的では、GNN による予測値も一定程度有用か

学習に伴う損失関数の推移（水平載荷）#

水平載荷の場合で GCN と GAT の比較を行った
同一の時間（ 24h ）で計算できたエポックまでで比較したところ、学習データではそれほど大きな差はないものの、テストデータでは GAT のほうが良い結果を示した

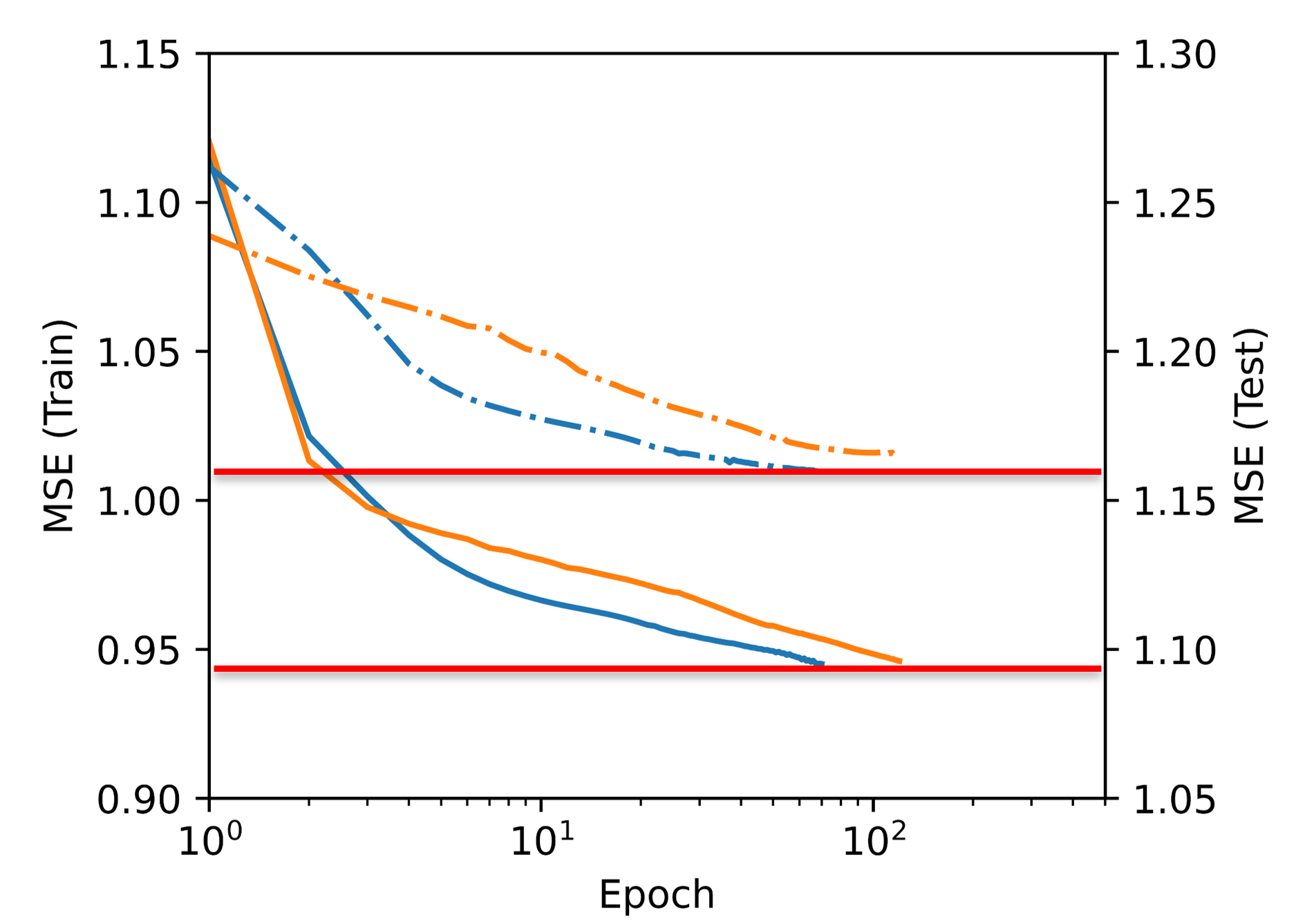
※いずれも目的変数は u_x と u_z のみ

予測結果の一例( $𝒖_𝒙$ and $𝒖_𝒛$ )：水平載荷、SmallRelu#

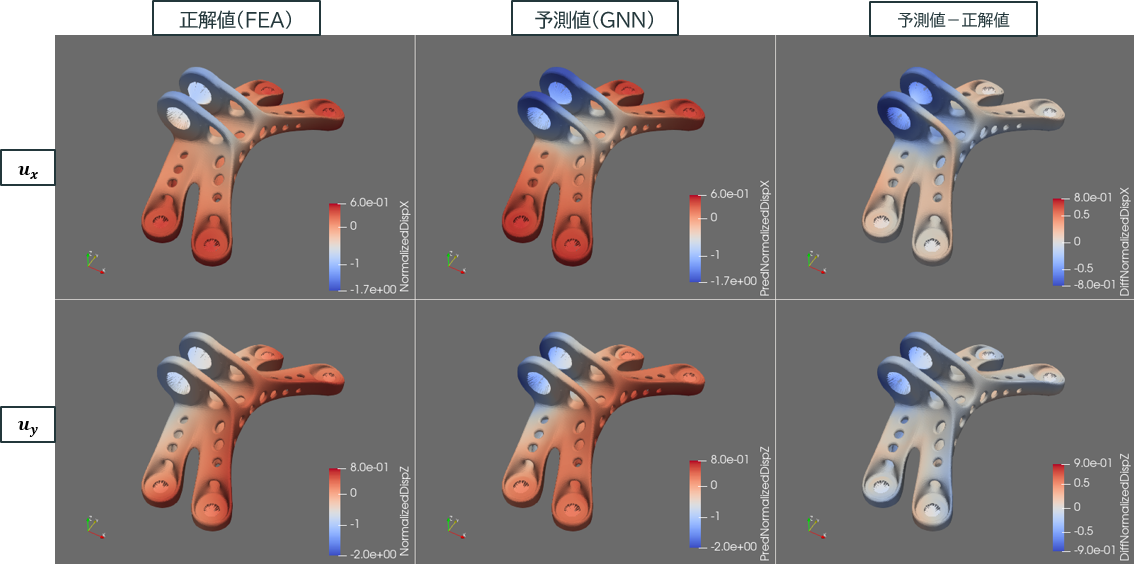
目的変数は u_x と u_z のみ

まとめ#

グラフニューラルネットワーク (GNN) のサロゲートモデルを用いたジェットエンジンブラケット (JEB) の数値解析を実施した。
SimJEB データセットのメッシュファイルを利用し Advance/FrontSTR による計算結果をグラフデータに変換し、データセットを作成することができた。
作成したデータセットを用いて、GATConv 層を含むようなネットワークで学習を行った
学習させたモデルは、変位や Mises 応力について、正解値と大まかに同様の傾向を示す結果を推定することに成功した。
ただし十分な精度良い推論とするには、モデルの構成やノーマライズの方法を調整するなどの課題が考えられる。