点音源からの放射#
点音源からの放射について、完全吸収境界の与え方を変えた2つのモデルで解析を実行し、解析結果を比較しました。 この例は、ソフトウェア同梱のチュートリアルのDに対応します。
2種類の完全吸収境界#
Advance/FrontNoise では、2種類の完全吸収境界が利用可能です。
- ρc境界:インピーダンス境界の一種で、音響インピーダンスを特殊な値(; 密度×音速)に設定することにより、面に入射した音波による反射をなくすものです。ただし、反射がなくなるのは面の法線方向の成分のみです。
- 無限要素:基礎方程式に無限遠点での境界条件 (Sommerfeld radiation condition) を課した式を解くことにより、面に入射した音波による反射を完全になくすものです。ただし、この面は球面の一部である必要があります。
解析条件#
解析条件の概要は次のとおりです。 以降、『ρc 境界』、『無限要素』はそれぞれの境界条件を使用するケースに対するケース名を意味します。
| 項目 | 条件 |
|---|---|
| 解析領域 | 『ρc 境界』:半径 1.5m の球 『無限要素』:半径 0.5 m の球 |
| 音源 | 球の中心にある体積速度を与える(点音源) |
| 境界条件 | 『ρc 境界』:球の表面すべてを ρc 境界による無反射境界 『無限要素』:球の表面すべてに無限要素を定義 |
| 音速 | 300 m/s |
| 密度 | 1.0 kg/m3 |
| 解析周波数 | 400 Hz のみ |
『ρc 境界』のメッシュは 117,772 節点、671,119 要素で、 『無限要素』は 5,312 節点、27,389 要素です。 両者の差は解析領域の体積に由来します。 どちらもメッシュサイズは 5 cm です。
| 解析形状(黄色の『ρc 境界』と緑の『無限要素』を重ねて描画している) |
|---|
 |
解析結果#
断面の音響速度ポテンシャル#
両者の音響速度ポテンシャルの実部を可視化したコンター図を示します。 これらの描画範囲は半径 1.5m の球の断面です。 『無限要素』ではメッシュが存在するのは半径 50cm までですが、その外側についてもソフトウェアに付属するユーティリティツールを利用することで、メッシュが存在する部分と同様に値の取得や可視化が可能です。
| ρc 境界 | 無限要素 |
|---|---|
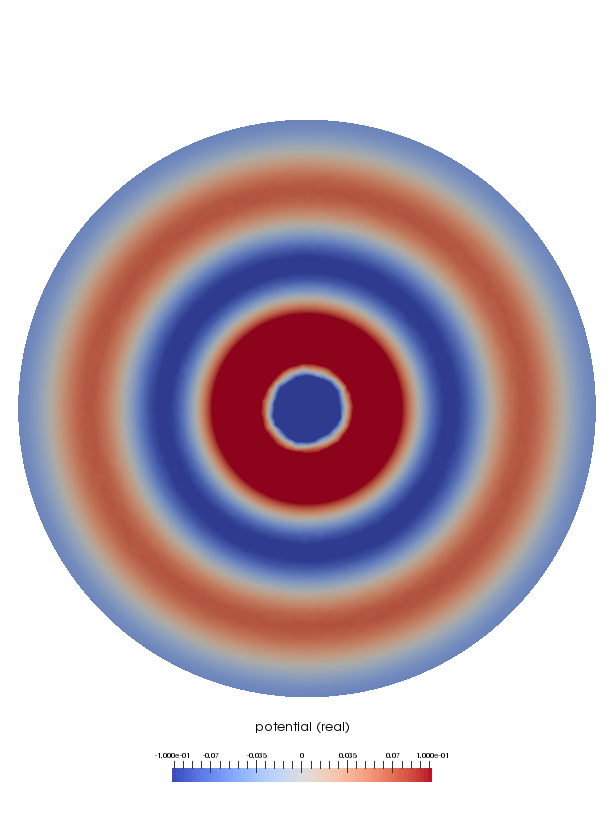 |
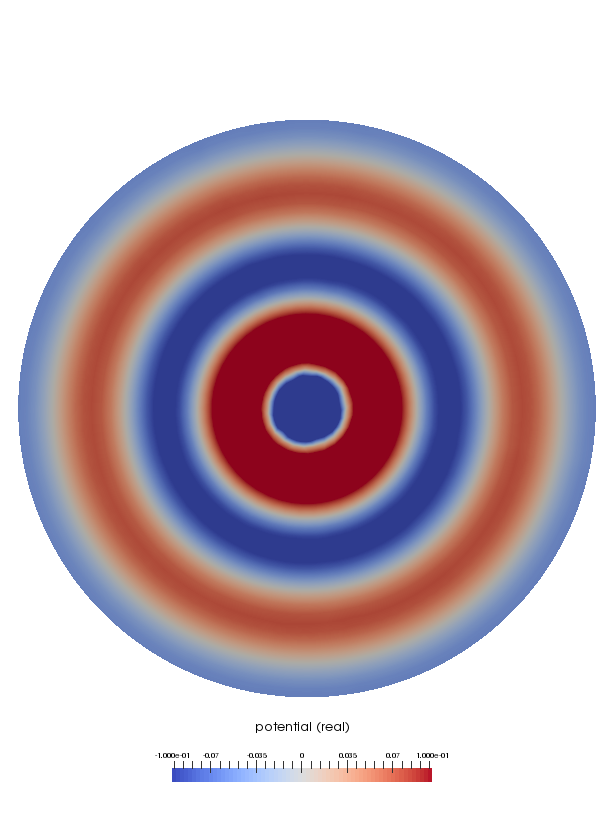 |
線上の音響速度ポテンシャル#
次に、座標軸上の音響速度ポテンシャル(実部 real, 虚部 imag)を比較しました。 図中の case11 が『ρc 境界』で、case21 が『無限要素』です。 両者は定量的によく一致しています。
| 軸上 () | 軸上 () |
|---|---|
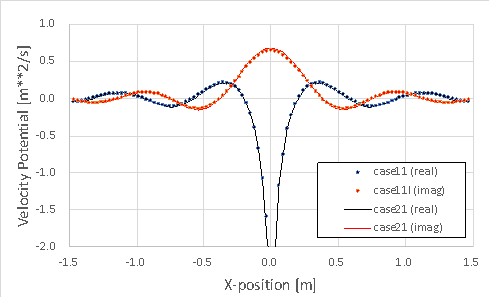 |
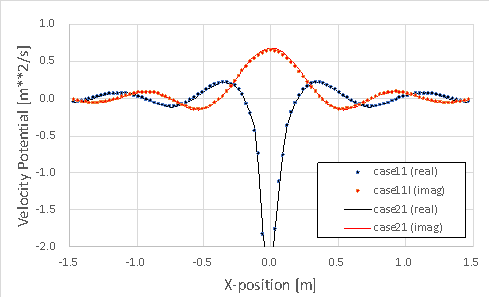 |
解析解との比較#
また、この問題には解析解が存在します。
ここで、, , , , はそれぞれ音響速度ポテンシャル、音源からの距離、体積速度(点音源の強さ)、周波数、音速です。 前述の結果はこの解析解ともよく一致することを確認しました。
計算時間#
ここまでで2つのケースの結果と解析解がよく一致することを確認しました。 『無限要素』を採用する大きなメリットとしては、計算時間の短縮があります(表はある環境における測定値)。
| ケース | 体積の比 | 計算時間 |
|---|---|---|
| ρc 境界 | 27 | 約 30 秒 |
| 無限要素 | 1 | 約 1 秒 |
前述の通り、『無限要素』では音源から評価点までのメッシュを作成する必要がないため、解析規模の大幅な削減や、それによる計算時間の短縮が可能になります。
その他#
本ページで紹介したケースでは球の中心と音源が同一の場所にありますが、そうでない解析も実施可能です。 ただし、『ρc 境界』では球面の法線方向と音源の方向が一致しない場合が増えるため、若干の差が発生します。