コンテンツにスキップ

超高圧と超低圧が混在する管路系流体解析#

管路系流体解析ソフトウェア　Advance/FrontNet 事例

解析モデルと条件#

図1のように両端にタンクが設置されている管路系にて、バルブを全開にして断熱圧縮の過程を計算します。初期条件は、N2タンクは超高圧の30.1 MPaA、O2タンクは低圧の0.1 MPaAと超低圧の1.0 PaA、1.0×10-3 PaAの3ケースについて実施します。Advance/FrontNet/Γでは、実在物性用理想気体型状態方程式を扱えるため、比較のために実在物性用のデータベースNIST/REFPROP、完全理想気体および実在物性用理想気体型状態方程式を適用して計算結果の比較を行います。なお、NIST/REFPROPは、超低圧が適用範囲外であるため、O2タンクの初期条件が超低圧の計算ケースでは適用していません。
超低圧では摩擦圧損が非現実的な過大評価となるため、文献(1)(2)を参考にKnudsen数に応じて滑り領域を考慮した摩擦係数に乗じる係数を算出するモデルを作成しています。

図1 計算モデル

図1 計算モデル

解析結果#

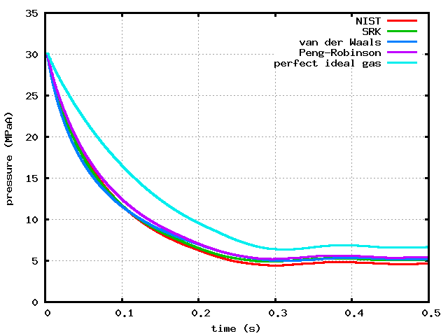
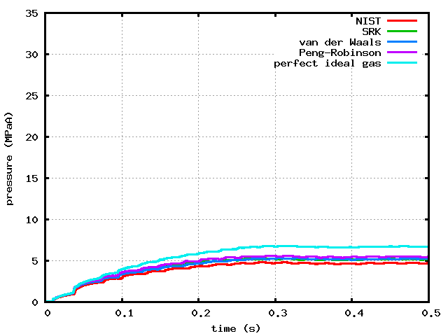
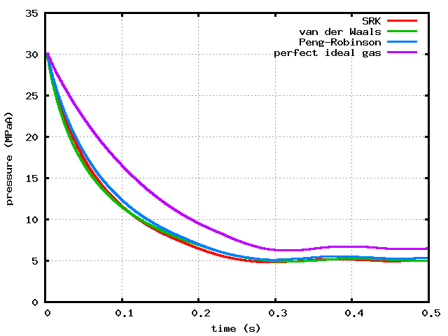
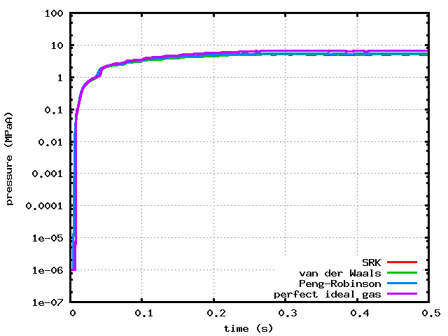
計算結果を図2に示します。O2タンクが低圧のケースでは、0.35 s程度で流れが定常になっていることが分かります。また、O2タンクが超低圧のケースでも同様の結果が得られていることから、超低圧の条件でも適切に計算できることが分かります。なお、O2タンクの圧力がとても低いことから、縦軸を対数として表示しています。
各状態方程式の計算結果を比較すると、両ケースとも、完全理想気体方程式は実在物性用の方程式と比べて圧力が高いこと、実在物性用の方程式はどのモデルも同じような圧力推移になっていることから、実在物性用の方程式は分子間力と分子の占める体積が計算に反映されていることが分かります。

計算ケース N2タンク圧 O2タンク圧
O2タンク低圧
(0.1 MPaA)		 case1-N2 case1-O2
O2タンク超低圧1
(1.0 PaA)		 case2-N2 case2-O2
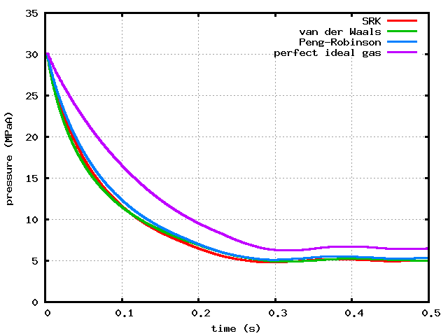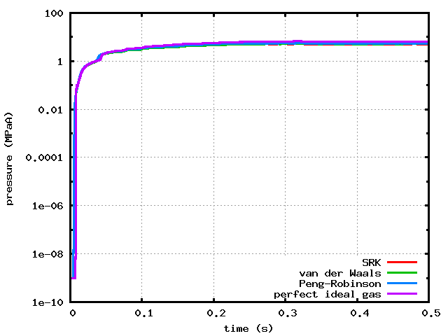O2タンク超低圧2 (1.0×10-3 PaA) case3-N2 case3-O2

図2 各タンクの圧力変化

参考#

(1)https://ja.wikipedia.org/wiki/%E5%B9%B3%E5%9D%87%E8%87%AA%E7%94%B1%E8%A1%8C%E7%A8%8B (2)https://ja.wikipedia.org/wiki/%E3%82%AF%E3%83%8C%E3%83%BC%E3%82%BB%E3%83%B3%E6%95%B0

関連ページ#