Soret 効果の解析事例#
概要#
Soret 効果（Ludwig-Soret 効果）とは、混合溶液に温度勾配を与えて放置しておくと濃度勾配が生じるという現象に見られるように、特定の成分が高温側または低温側に拡散し濃縮される熱拡散のことです。濃度勾配による濃度拡散と温度勾配による濃度勾配が平衡状態に達する場合は拡散平衡となります。[1]
解析条件#
図 1 のように二酸化炭素と水素の混合ガスが充填された平板空間を考えます。平板空間の上部には低温壁、下部には高温壁があるものとして、Soret 効果による濃度拡散の様子を見ます。
図 1. 解析モデル#
| 項目 | 設定 |
|---|---|
| 平板のサイズ | XY 平面で横 10 m, 縦 5 m |
| 低温壁の温度 | 273 K |
| 高温壁の温度 | 723 K |
| 初期の温度勾配 | 450 |
| 二酸化炭素の質量分率 | 50 % |
| 水素の質量分率 | 50 % |
| 初期の濃度勾配 | 0 |
| 熱拡散係数 | 経験的な組成依存式[2] |
| 重力加速度 | 9.8 m/s と 0 m/s の 2 通り |
解析結果#
Soret 効果により低温側に二酸化炭素が高温側に水素が移動します（図 2）。濃度勾配が低温側と高温側で異なるのは、熱拡散係数が温度や分子量、質量分率、モル分率によって異なるためです。重力がある場合は、低温側に移動した二酸化炭素が重力の影響を受けて落下します。これは、Rayleigh-Taylor 不安定性に相当します。このとき、流体の運動による物質拡散と濃度勾配による物質拡散、温度勾配による物質拡散が競合した状態になります（図 3, 4）。なお、図 3, 4 で Rayleigh-Taylor 不安定性が中央付近で顕著に発達しているのは、この部分のメッシュサイズが細かく波長の短い波が表現できているからです。Rayleigh-Taylor 不安定性は波長が短いほど成長率は大きくなります。
図 2. 重力がない場合（カラーは二酸化炭素の質量分率、グラフは白線部分の断面図）#
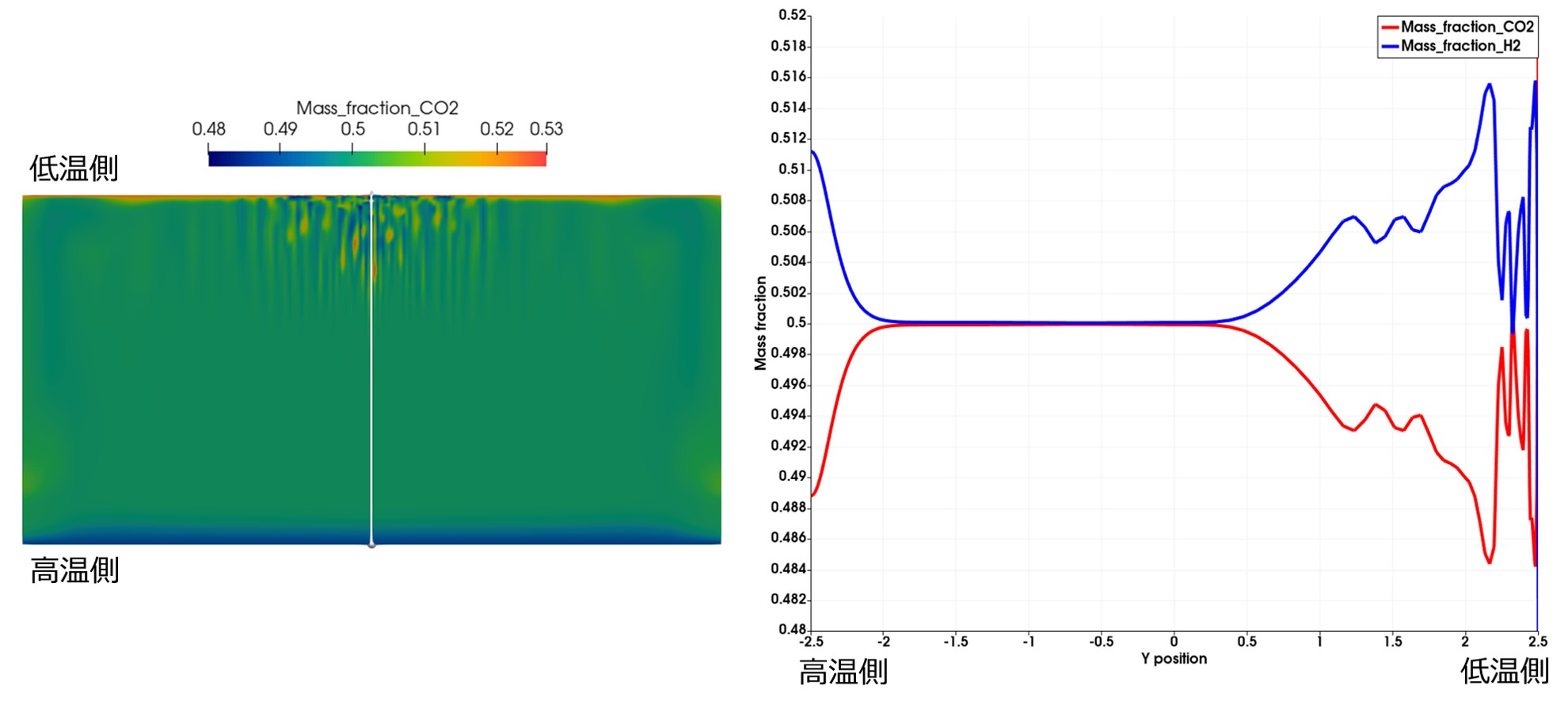
図 3. 重力がある場合（カラーは二酸化炭素の質量分率、グラフは白線部分の断面図）#
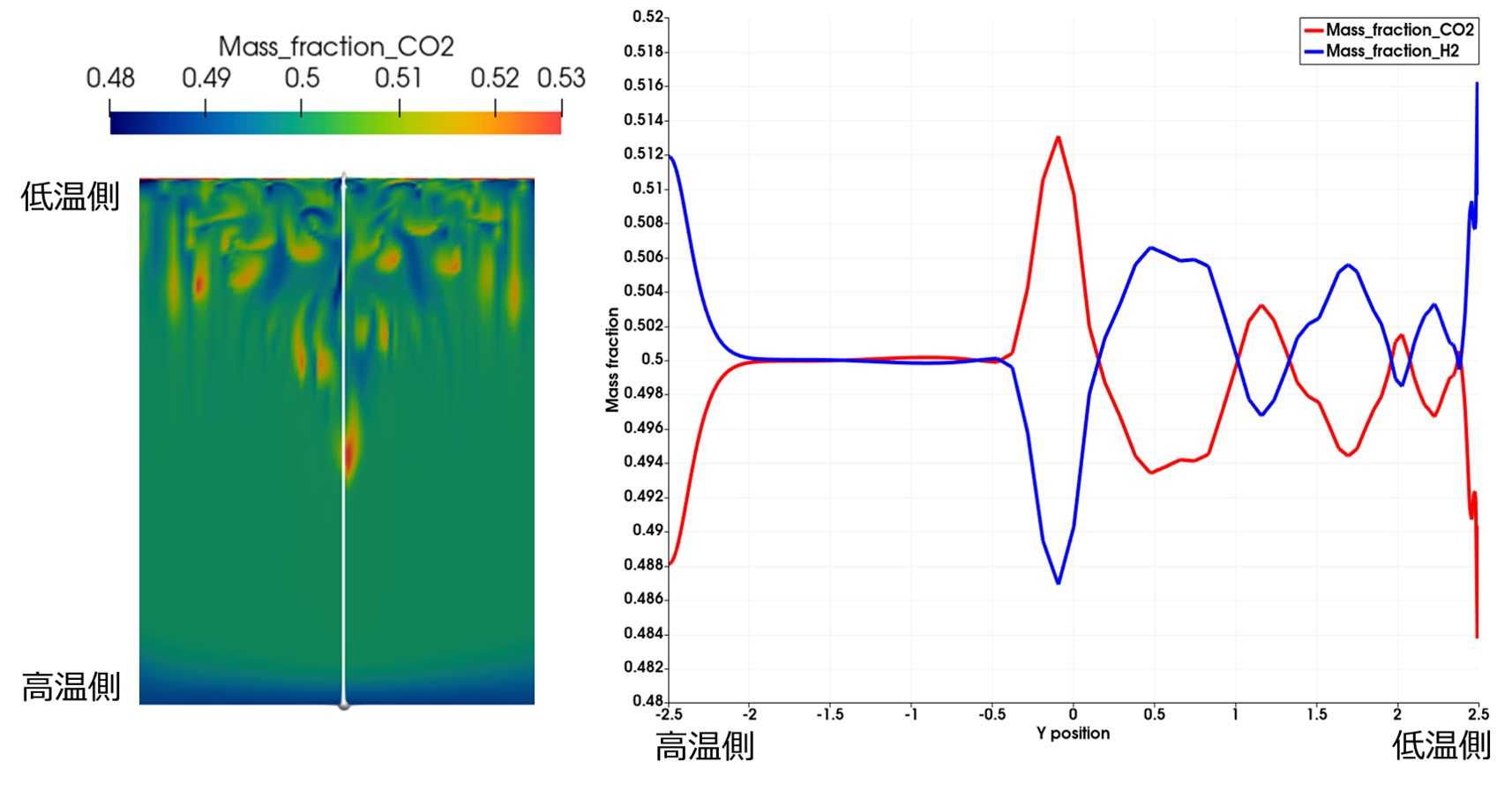
図 4. 重力がある場合（図 3. より後の時刻、計算領域の中央部分を拡大して表示）#
適用例#
例えば、Soret 効果である温度勾配による物質拡散のみを利用して、混合ガスを分離する装置[3]が提案されています。
参考文献#
[1] 岩石学辞典 岩波書店
[2] K.K.Kuo, Principles of Combustion (1976)
[3] 小野直樹ら「温度差のみで流体の成分分離を実現する小型デバイス」科学技術振興機構 新技術説明会（スマートQOL）2016
関連ページ#
- 流体解析ソフトウェア Advance/FrontFlow/red
- 解析分野：流体
- 産業分野：材料・化学