非ニュートン流体の粘性モデル#
概要#
非ニュートン流体は、力の加え方(速さや強さ)によって、粘度(ドロドロ具合)が変化する流体のことです 。身近な例では、水や油は力を加えても粘度が一定の「ニュートン流体」ですが、ケチャップやペンキは非ニュートン流体です。以下の図 1は非ニュートン流体の性質を分類するための代表的なモデルを示しています 。Newtonian Model (ニュートン流体)は原点を通る直線のグラフです。これは、加える力と変形の速さが常に比例し、粘度が常に一定であることを意味します(水、油、アルコールなど。)。Power Law Model (パワーローモデル)は、原点を通る曲線のグラフです。力が強くなる(速く動かす)につれて傾きが緩やかになっており、「粘度が低下する」性質(シアシニングまたは擬塑性)を示します(ペンキ、血液など)。Bingham Plastic Model (ビンガム流体)は、グラフが原点から始まらず、縦軸の途中から始まっています。縦軸の切片が「降伏応力」です。この一定の力を超えるまでは全く流れず(速さゼロ)、超えた後はニュートン流体のように粘度が一定になります(グリース、マヨネーズ、歯磨き粉など)。Herschel-Bulkley Model (ハーシェル・バルクレーモデル)は、ビンガムモデルとパワーローモデルを組み合わせたような性質を持ちます。「降伏応力」があり、それを超えて流れ出した後も、パワーローモデルのように粘度が変化します(コンクリート、合成樹脂など)。
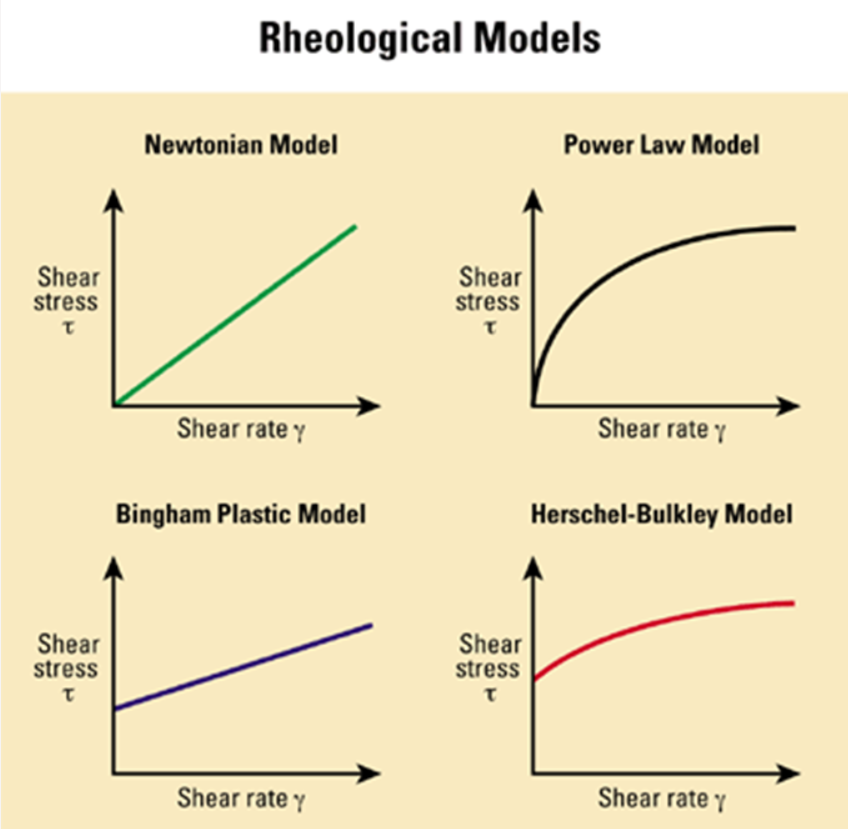
図 1. せん断速度とせん断応力の関係
解析手法(粘性モデルの組み込み)#
ニュートン流体では、流れのせん断応力と速度勾配(せん断速度)が比例するモデルを使用します。一方で、非ニュートン流体では、粘性係数が定数ではなく、せん断速度に依存するモデルを使用します。Advance/FrontFlow/redでは、Herschel Bulkleyモデルの式を追加し、粘性モデルを表します。モデル係数を調整することで、他のモデルも表現することが可能です。
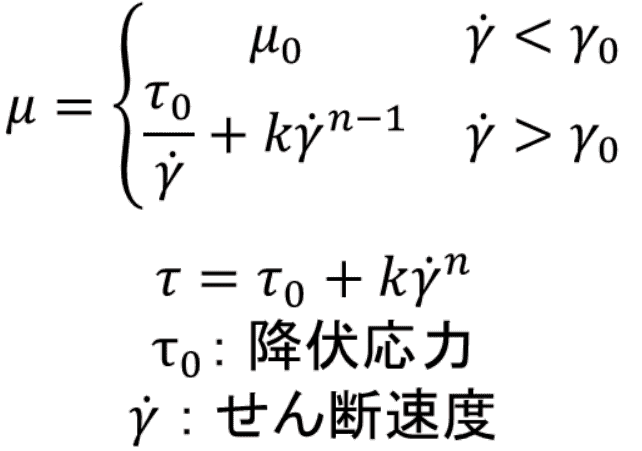
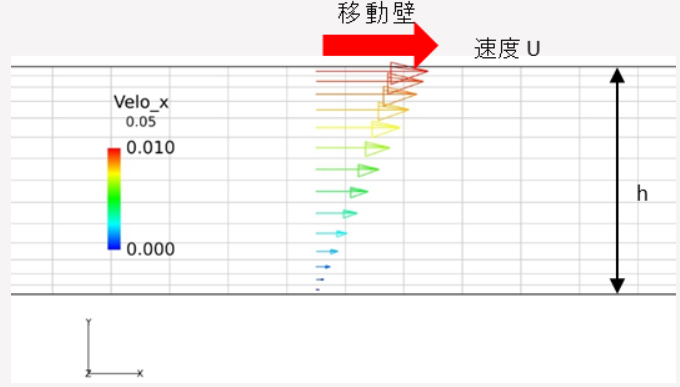
図 2. クエット流れの概要
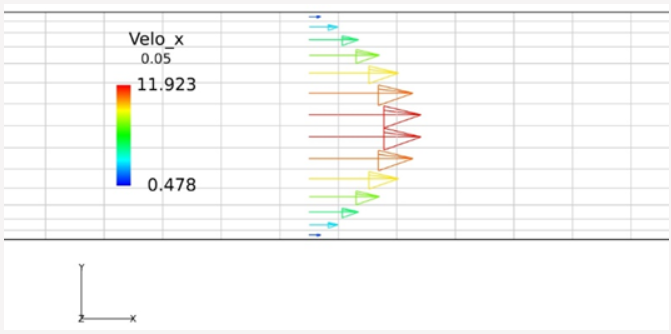
図 3. 平面ポアズイユ流れの概要
ここでは、
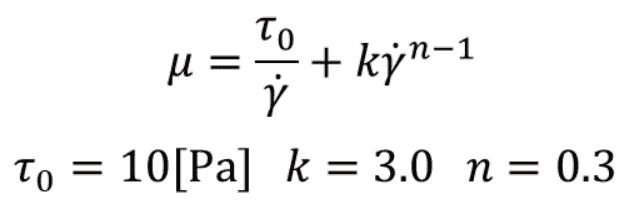
を使用した際の、クエット流れの解析結果を示します。せん断速度と壁面摩擦力の関係がHerschel-Bulkleyモデルの式を満たしていることを確認できました。
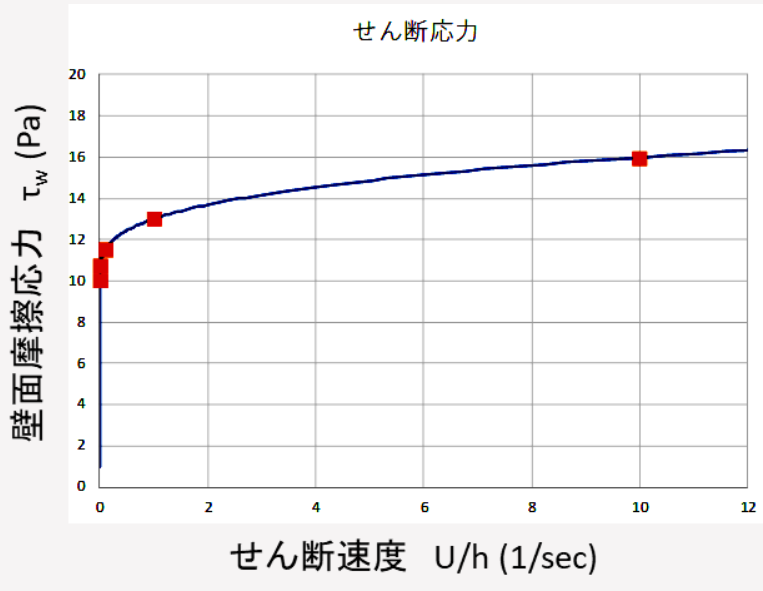
図 4. せん断速度と壁面摩擦応力の関係
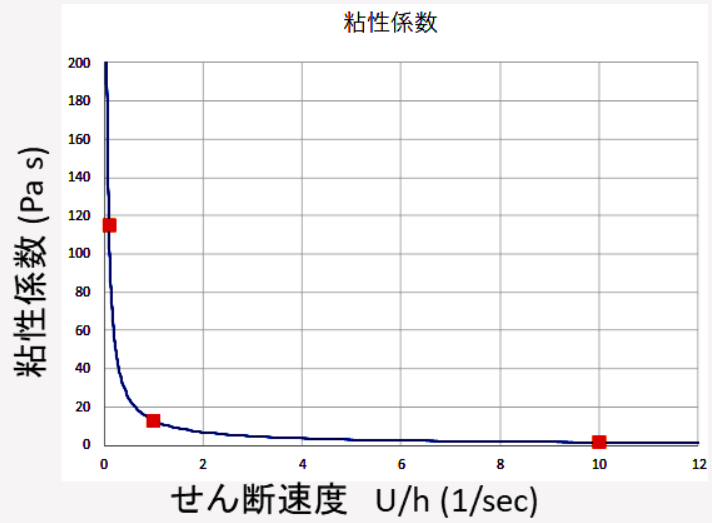
図 5. せん断速度と粘性係数の関係(線形領域)
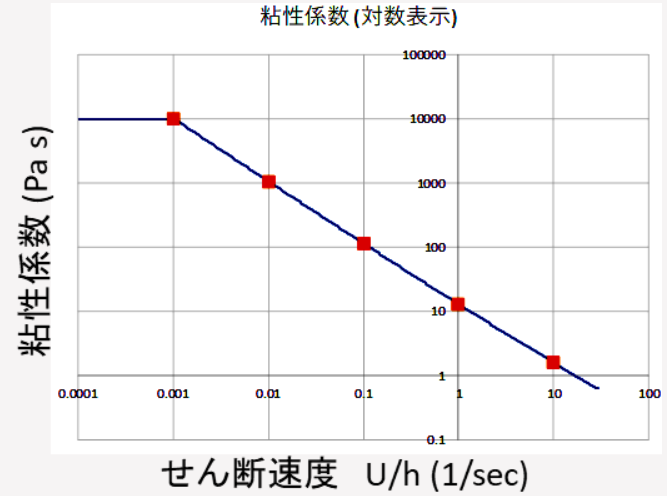
図 6. せん断速度と粘性係数の関係(対数領域)
続いて、平面ポアズイユ流れの解析結果です。ここでは、
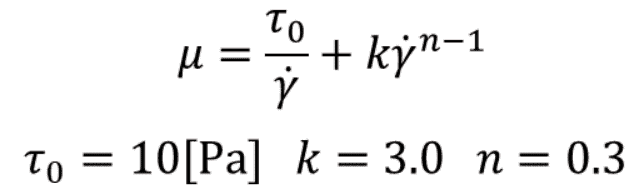
の関係式を用いて解析を行います。結果を確認すると、速度勾配に対して、粘性が一定ではないため、Herschel-Bulkleyモデルでは、壁面近傍では大きなせん断がありますが、中央部ではほとんどせん断が見られませんでした。
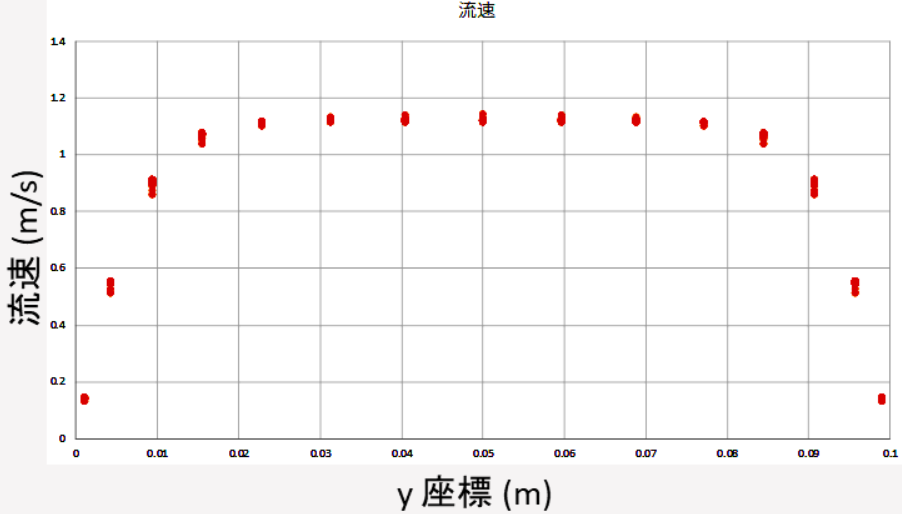
図 7. 高さ位置座標における流速分布
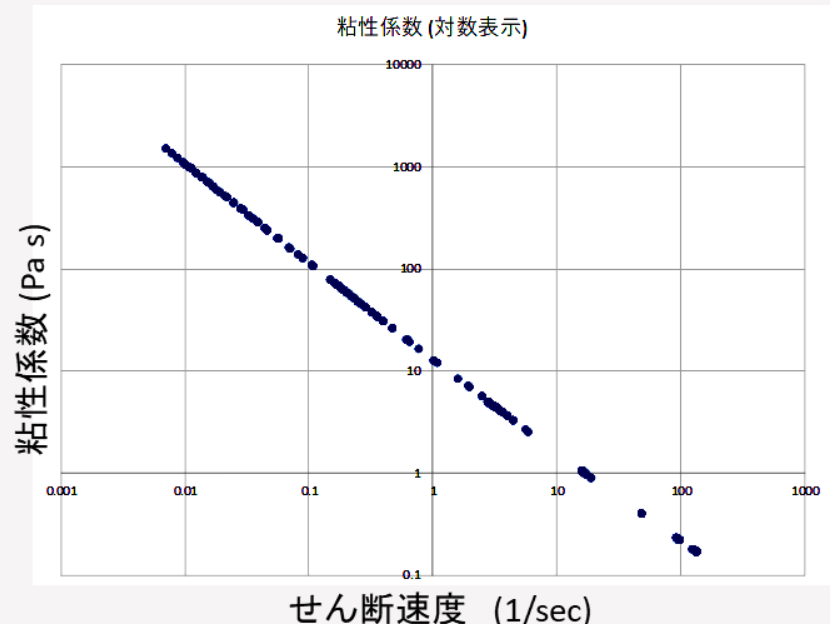
図 8. せん断速度と粘性係数の関係(対数領域)

図 9. 平面ポアズイユ流れにおける速度ベクトル分布
まとめ#
非ニュートン流体用の粘性モデルを組み込み、クエット流れ、平面ポアズイユ流れにおいて検証を行いました。