傾斜した矩形密閉空間の輻射-熱伝導-対流連成解析#
目的#
左壁面を等温度加熱し右壁面を等温冷却した矩形容器内の輻射-熱伝導-対流連成解析を行います。 輻射熱伝達の計算ではFVM法を使用します。コード内にはモンテカルロ法(Monte-Carlo)とゾーン法(Zone)も実装されています。
解析対象#
〇 形状 解析対象は、二次元の矩形密閉空間で、空間内は空気で満たされています(図 1)。
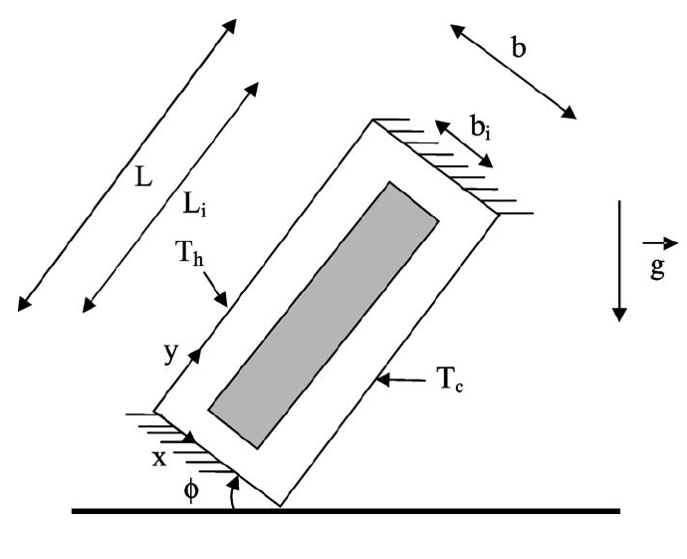
図 1. 解析対象図
〇 熱境界条件
密閉空間の長い方の壁は、それぞれ異なる一様な温度(高温壁 Th、および低温壁 Tc )に保たれています。 短い方の壁は断熱と見なされます(図1) 。
〇 傾斜
密閉空間は鉛直方向に対して傾斜角Φを持って配置されています。
解析条件#
この解析条件を表 1にまとめています。
表 1.解析条件表
| 項目 | 値 |
|---|---|
| 計算コード | Advance/FrontFlow/red |
| 輻射モデル | 有限体積法(FVM/DOM、Sn=6) |
| 計算領域 | b=0.03[m], L/b=2, Z/b=3, b_i/b=0.4, L_i/L=0.8 |
| 境界条件 | x=0, T=T_h, x=b, T=T_c, y=0, L, δT/δn-q_r=0, z=0, Z周期条件 |
| メッシュ | 6面体格子、セル数 30×40×60、50×100×60 |
| 計算パラメータ | Ra = 7.5×104, Pr = 0.70, T_0 = 300K |
また、パラメータ説明を以下にまとめます。

物体と密度、熱容量は流体と同一とする
解析結果 等温線図#
図2は、Z中心断面の等温線図の、輻射なし・傾斜角なし、輻射あり・傾斜角あり、輻射あり、傾斜角30°を文献とAFFrの解析結果で比較したものです。 等温線は、高温の左壁から低温の右壁に向かって、流動によって大きく歪んでいることがわかります。 特に、上部の角付近では熱い空気の層が停滞し、温度成層の傾向が強く見られます。
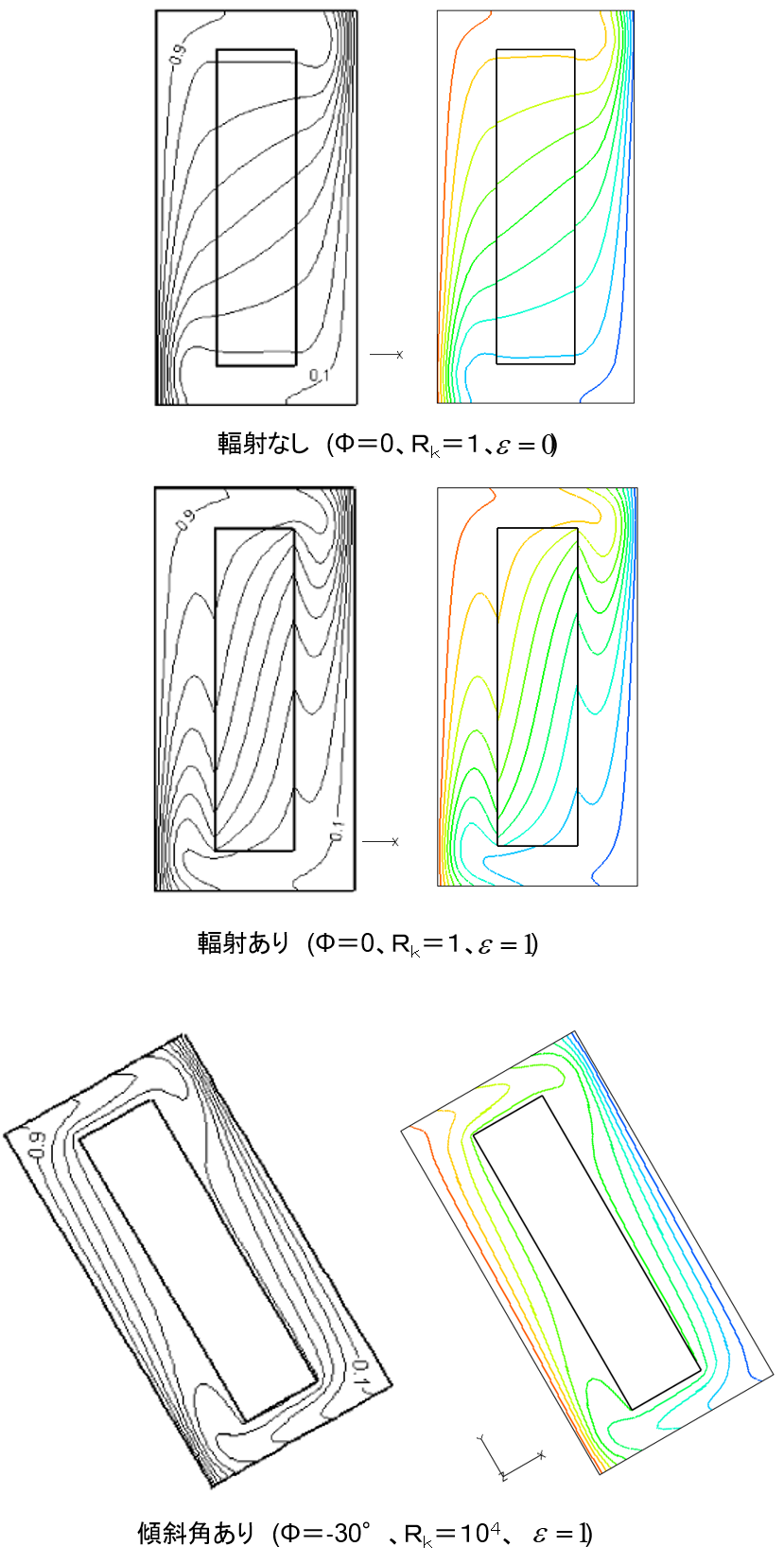
図 2. Z中心断面の等温線図
左の白黒の結果は文献[1]、カラーの結果は本計算、カラーは温度の高さを表示する。
解析結果 熱い壁面上でのヌセルト数(Nu)分布図#
図3は、熱い壁面上でZ方向中央断面のNu分布図です。文献[1]とメッシュ分割を変えた、本計算結果で比較しています。 本解析結果は、メッシュ分割を変えても、文献とよく一致していることがわかります。
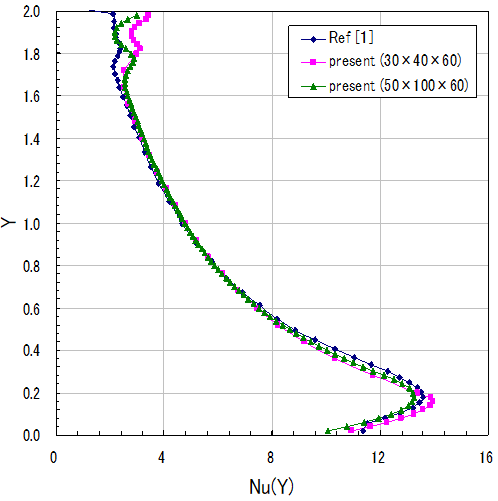
図 3. 熱い壁面上でZ方向中央断面のNu分布図 (Φ=0、R_k=1、ε=1)
解析結果 熱い壁面上の平均Nuwにおいて傾斜角度の影響#
図4は、熱い壁面上を平均ヌセルト数が、傾斜角によってどのように変化するかを示しています 。 傾斜角θ=-30°付近でNuwは最大値をとり、θ=60°付近で最小値を取ることがわかります。
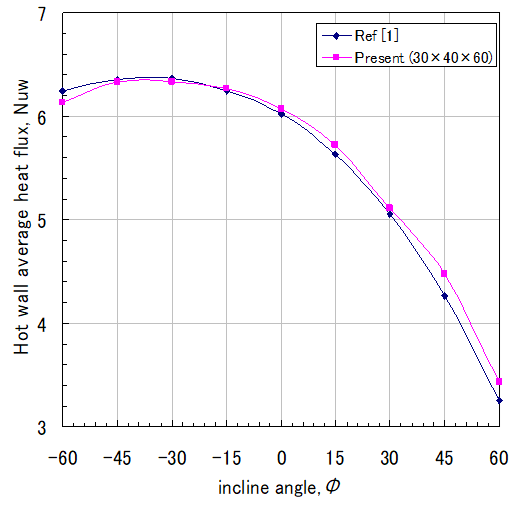
図 4. 熱い壁面上の平均Nuwにおいて傾斜角度の影響(Rk=1、ε=1)
図5は、密閉空間内に内蔵された物体の伝導率Rkが、熱い壁面上の平均ヌセルト数Nuwに及ぼす影響を示しています。
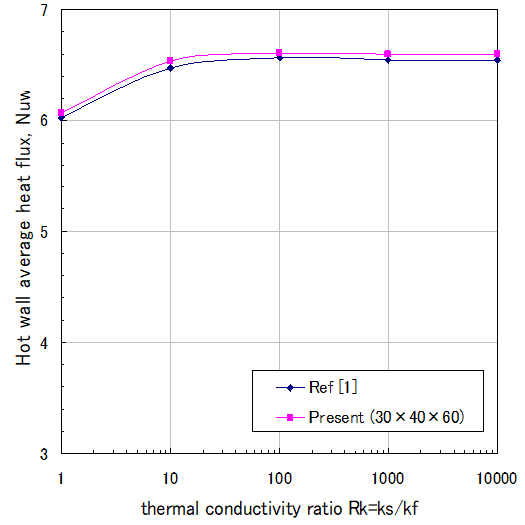
図 5. 熱い壁面上の平均Nuwにおいて物体熱伝導率の影響 (Φ=0、ε=1)
まとめ#
本解析は、Advance/FrontFlow/redで、傾斜した矩形密閉空間における表面輻射、熱伝導、自然対流の連成熱伝達を扱っています。その妥当性は、等温線図の傾向(図2)、垂直配置での局所ヌセルト数分布(図3)や、傾斜角(図4)および内部物体伝導率(図5)の影響に関する平均ヌセルト数の傾向で、論文とほぼ良好に一致することを確認しています。
(*)参考文献: [1] Bouali H., Mezrhaba A., Amaoui H., Bouzidi M. Radiation-Natural Convection Heat Transfer in an Inclined Rectangular Enclosure, Int. J. Thermal Sci., 45, 553-566, 2006.