時間積分法の基本検証#
概要#
本解析は、AFFrを用いて時間積分法(Euler陰解法、Crank-Nicolson法、Adams-Moulton法)の違いが、円柱周りの非定常層流解析における物理量の時間応答および精度に及ぼす影響を検証し、各手法の基本的な特性を確認することを目的とします。
解析モデル#
チャネル内円筒周りの層流を対象としています。解析領域を図 1 に示します。チャネルの高さは4.1m、解析領域の長さは22mで、中央に円筒が配置されています。流れは二次元層流として扱われ、円筒周りに発生するカルマン渦の挙動を評価します。節点数 44,756、要素数 32,784です。
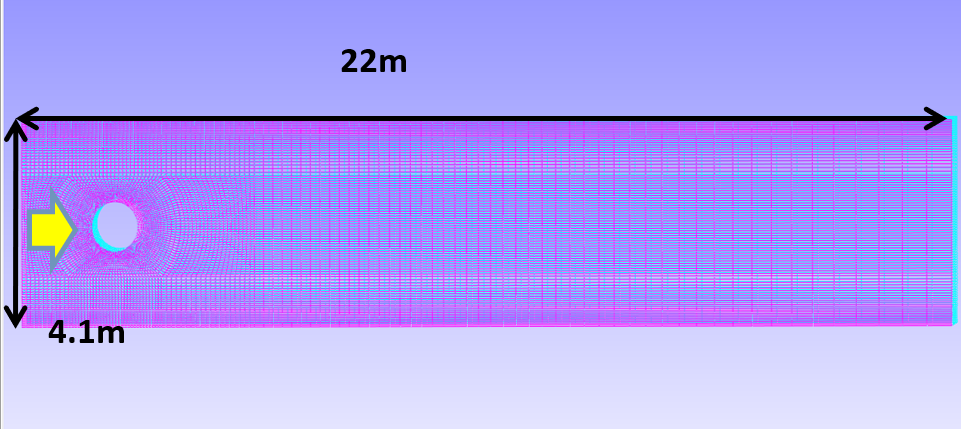
図 1. 解析領域
解析条件#
時間積分法として、Euler陰解法、Crank-Nicolson法、Adams-Moulton法の3種類を使用し、時間刻みは全て5.0-5secです。
解析条件を表 1にまとめています。
表 1. 解析条件
| 項目 | 設定 |
|---|---|
| 入口速度 |
円筒を中心とした放物型 (600/4.1)*[(y+2)*4.1-(y+2)2] (yは下面からの距離) |
| 差分スキーム | 2次中心差分 |
解析結果#
図2に解析結果を示します。Crank-Nicolson法による速度場と圧力場の瞬時値から、カルマン渦の規則的な放出が確認されます。抗力係数および揚力係数の時間変化は、3つの時間積分法で同様の周期的変動を示しており、既往の研究結果であるStrouhal数 St=0.3018の揚力係数周期0.0332secを再現しています。グラフの比較では、Euler陰解法がわずかに異なる振幅を示すものの、全体として各手法が非定常現象を捉えられていることが示されています。
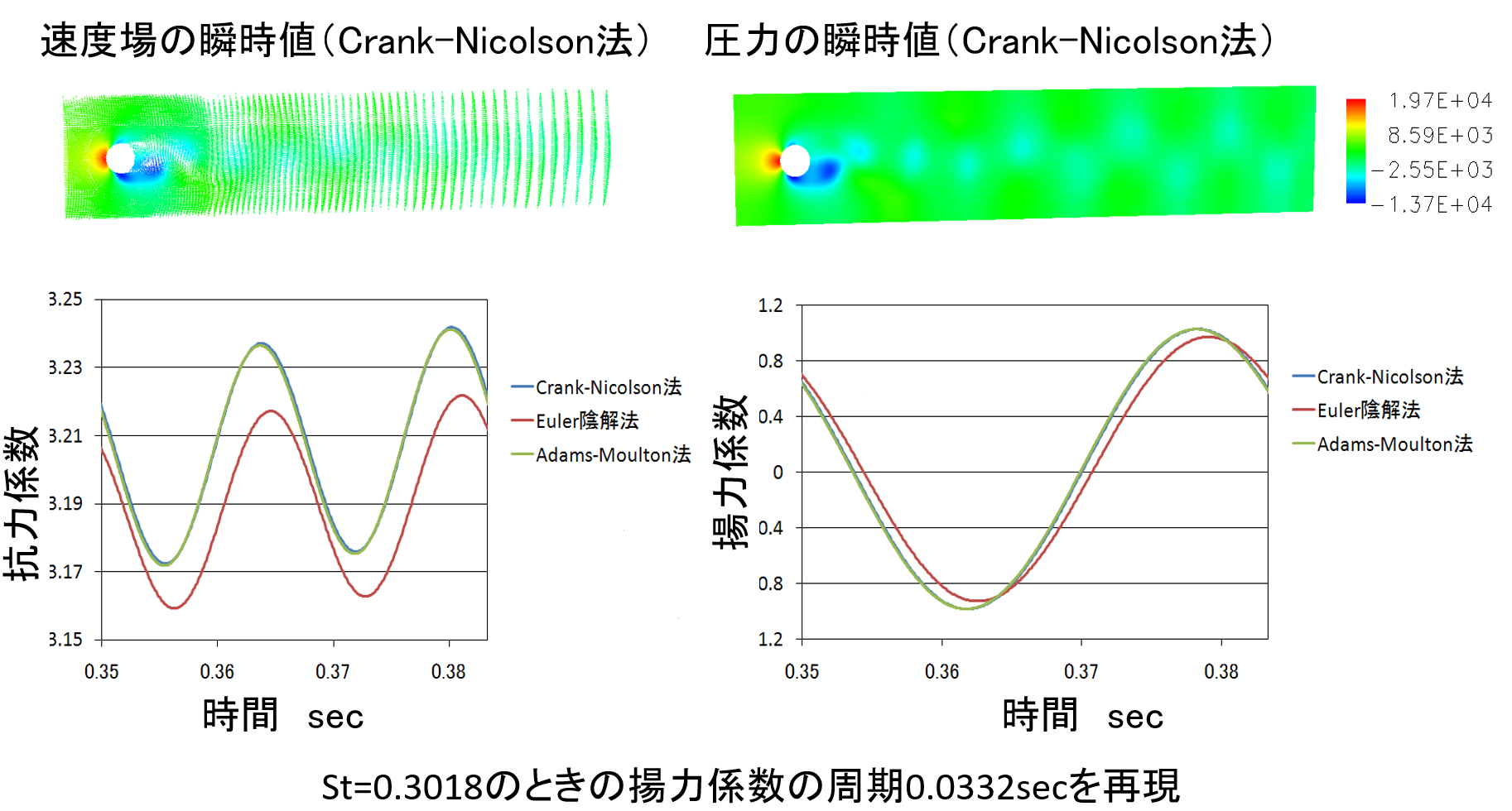
図 2.解析結果
まとめ#
本検証により、流体解析ソフトウェアAFFrに実装された主要な時間積分法が、円筒周り流れの非定常現象を適切にシミュレーションできることを確認することが出来ます。特に、Crank-Nicolson法とAdams-Moulton法は非常に近い結果を示し、高い精度と安定性を持つことがわかります。
(*)参考文献:”ファーツィガー,ペリッチ,コンピューターによる流体力学”,シュプリンガー・フィアラーク,pp250,2003.