ベクトル計算機(NEC SX-Aurora TSUBASA)におけるAdvance/FrontFlow/redの高速化#
概要#
NEC SX-Aurora TSUBASAとは、PCIeカード型ベクトルエンジンです。一般的なサーバーやワークステーションに搭載されているPCI Expressスロットに、グラフィックボードのように増設できるカードの形をしており、これにより、既存のPCサーバーにスーパーコンピュータ級の計算能力を追加することが可能です。
NEC SX-Aurora TSUBASAを図 1 に示します。

図 1. NEC SX-Aurora TSUBASA (https://jpn.nec.com/hpc/sxauroratsubasa/より)
一般的なCPUが行う計算方法がスカラー計算です。データを一つずつ順番に処理していくため、シミュレーションのような膨大なデータ処理には時間がかかります。対して、SX-Aurora TSUBASAが得意とする計算方法がベクトル計算です。大量のデータを一度にまとめて処理します。例として256個のデータを一括で処理でき、圧倒的な効率化が可能です。このような「ベクトル化」により、特にシミュレーションやAI、ビッグデータ解析といった、膨大なデータ処理が求められる分野で絶大な性能を発揮します。
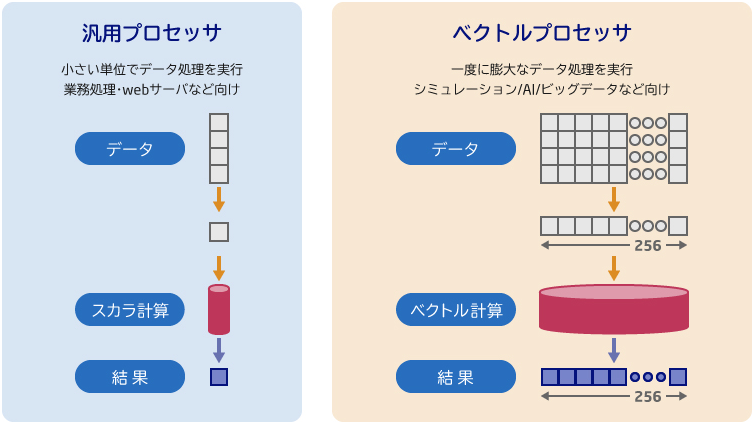
図 2. スカラー計算とベクトル計算の違い (https://jpn.nec.com/hpc/sxauroratsubasa/features/index.html#anc-features-aより)
高速化手法#
Advance/FrontFlow/redではSemi-Implicit Method for Pressure Linked Equations algorithm (SIMPLE法)というアルゴリズムを用いています。このアルゴリズムでは、計算時間の大半を占める圧力ソルバのベクトル化が必須となります。圧力ソルバ内では、巨大な連立一次方程式を解く計算を行っており、その計算を高速かつ安定させるためのが前処理が行われます。その代表的な手法として以下の2つが挙げられています。
・Incomplete Cholesky (IC) 分解:不完全コレスキー分解。強力でよく使われる前処理法です。以下のような数式で表され、Lの完全Cholesky分解の近似解を採用しています。
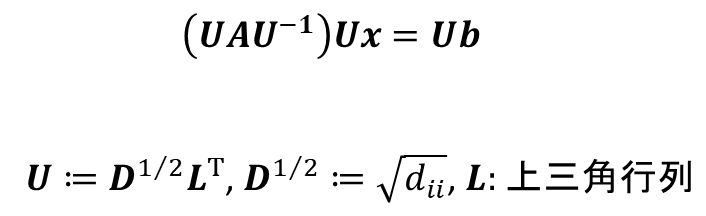
・Orthogonal scaling (OS) 法:直交スケーリング法。IC分解を単純化した手法です。以下のような式で表され、IC法においてL=Iとして解析を行います。
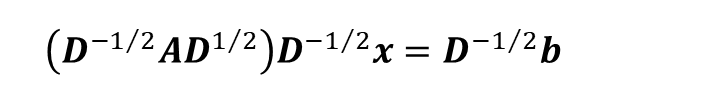
強力な前処理法である IC分解は、その計算過程で「前進・後退代入」というアルゴリズムを必要とします。この計算は、「1番目の計算結果を使って2番目を計算し、2番目の結果を使って3番目を計算する…」というように、本質的に逐次的(順番通りに進める必要がある)な性質を持っています。一方で、ベクトル計算機が得意なのは、大量のデータを一度にまとめて並列処理することです。そのため、逐次的な処理を苦手としており、IC分解をそのまま実装しても性能が上がらず、ベクトル化が困難という問題がありました。
この課題を解決するために導入されたのがMulti colour (MC) 法(マルチカラー法)です。これは、計算する点の順番を工夫する手法です。例えば、計算点をチェス盤のマスのように赤と黒に塗り分けたとします。赤のマスを計算するのに必要なのは隣の黒マスのデータだけなので、全ての赤マスを一度に(並列で)計算できます。次に、全ての黒マスを一度に計算します。このように計算の依存関係を解消し、データをまとめて処理できるようにすることで、逐次的な計算をベクトル計算機が得意な形に変換し、ベクトル演算が可能な前処理を実現します。
ベンチマーク解析#
解析対象は単体単純形状建築物モデルで、現実の複雑な都市ではなく、単純な四角い箱型の建物を1つだけ置いた、ベンチマークテストでよく用いられる標準的なモデルです。全て四面体要素を用いて解析を行い、節点数が約100万、要素数が約530万となっています。ここでは、SX-Aurora TSUBASA1台(1VE)を、8並列の構成で使用して計算しました。
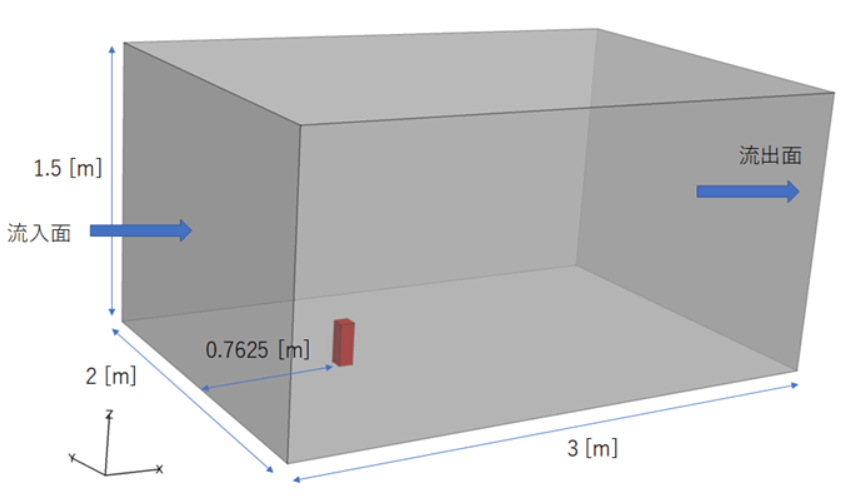
図 5. 解析領域
解析手法を表 1にまとめています。
表 1.解析手法
| 項目 | 設定 |
|---|---|
| 支配方程式 | 非圧縮性 Navier–Stokes 方程式 |
| 乱流モデル | Large Eddy Simulation (LES) 標準Smagorinskyモデル |
| 離散化法 | セル中心有限体積法 |
| 差分スキーム | 2次精度中心差分 |
| 時間積分法 | Crank–Nicolson法 |
境界条件を表 2にまとめています。
表 2.境界条件
| 境界 | 設定 |
|---|---|
| 流入境界面 | 適切な風速の鉛直分布と乱れの強さの流入変動風 |
| 流出境界面 | 自然流出境界 |
| 側面・上面 | 壁境界,流速 フリースリップ条件 |
| 地面 | 壁境界,流速 ノースリップ条件 |
| 建物 | 壁境界,流速 ノースリップ条件 |
解析結果#
図6は、解析結果よりスパン中央断面における流速分布を示しています。建物の前面では、流れが衝突して流速が低下するよどみ領域が形成されています。屋根上を流れる空気は局所的に加速し、建物の後方には流れが剥離したことによる低速で乱れの強い後流(ウェイク)領域が発生していることが分かります。この結果は、風による典型的な空気の流れ(剥離・再循環)をLES解析によって捉えていることがわかります。

図 6. 解析結果 スパン中央断面における流速分布
ベクトル化パフォーマンス#
準定常的な流れを維持するために、粘性による抵抗(摩擦)を打ち消す外力項を加えています。
以下の表3は、パフォーマンス測定結果を示しています。ベクトル化に対応していない従来の手法であるIC法では、ベクトル化率が低く、計算に7,860秒かかっています。一方で、ベクトル化に対応したMC法・OS法ではベクトル化率が98%以上に劇的に向上し、計算時間が約808秒にまで短縮されています。この結果から、MC法およびOS法はベクトル計算機において非常に高い計算効率を発揮することがわかります 。
表 3.ベクトル化前後の比較
| 100 steps | MFLOPS per core | ベクトル化率 | 平均反復回数 | 計算時間 (秒) |
|---|---|---|---|---|
| Before (IC法 ×8) | 1707 | 58.97 | 722 | 7860 |
| After (MC法 ×8) | 3761 | 98.19 | 798 | 808 |
| After (OS法 ×8) | 3921 | 98.67 | 1785 | 858 |
表4は、スカラー計算機とベクトル計算機の計算時間(Real Time)の比較を表にまとめたものです。 100step計算した結果では、スカラー計算機における計算時間が1521秒かかったのに対して、ベクトル計算機では688秒で計算が完了し、全体としても高速な結果が得られています。
表 4.スカラー計算機とベクトル計算機の計算時間の比較
| 100 steps | 計算時間(Real Time) (秒) |
|---|---|
| Advance/FrontFlow/red スカラー計算機 (Intel Xeon Gold 5218 CPU ×2) (32並列) | 1521 |
| Advance/FrontFlow/red ベクトル計算機 (NEC SX-Aurora TSUBASA 1VE) (8並列) | 688 |
次にストロングスケーリングの測定結果を示します。これは、これは、解析する問題の全体の規模は固定したまま、計算に使用するプロセッサの数(ここではrank数)を増やしていくと、どれだけ性能が向上するかを見る指標です。理想的には、プロセッサ数を2倍にすると計算時間は半分になります。ここでは、最大4台のベクトルエンジン(4VE)を使い、32並列(32 ranks)まで実行されました。
図7のグラフは、横軸が計算に使うプロセッサの数(Number of ranks)、縦軸が計算にかかった時間(解析時間)を対数で示しています。点線が理想的な性能向上を示しており、プロットされた点がこの線に近いほど、並列化の効率が良いと言えます。グラフを見ると、rank数を32まで増やしたときに、解析時間が約1/10になっています。これは「32並列で10倍程度の並列化効率」であり、良好なスケーリング性能を示していると言えます。MCCG(マルチカラー共役勾配法)とOSCG(直交スケーリング共役勾配法)という2つの手法で測定されており、rank数によって得意不得意が見られます。MC法とOS法を使い分けることで、さまざまな条件でより高い解析性能を発揮できます。
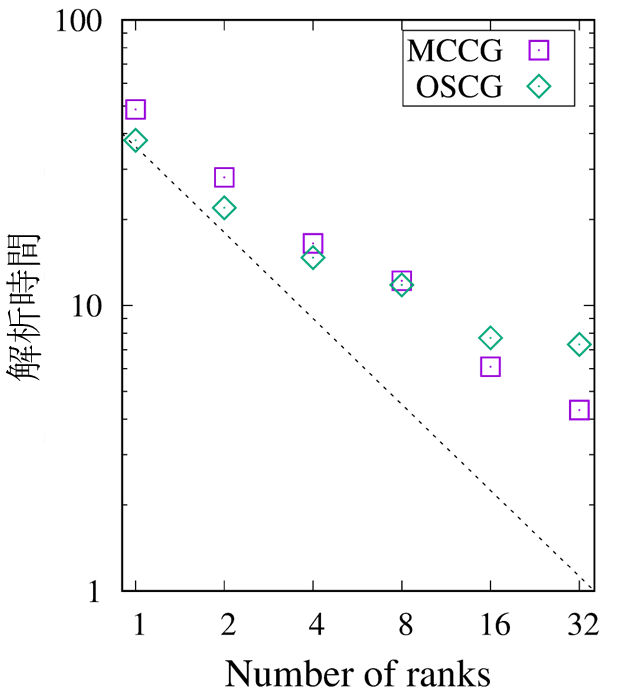
図 7. 解析結果 並列計算におけるストロングスケーリング