単独翼周りの2次元キャビテーション解析#
概要#
キャビテーションは、船のスクリューやポンプの羽根車のように、液体が高速で流れる場所で発生する現象です。液体の流れが急激に加速されると、その部分の圧力が低下します。この圧力が、その液体の温度における飽和蒸気圧を下回ると、液体はまるで沸騰したかのように気化し、内部に蒸気で満たされた無数の気泡(空洞=キャビティ)が発生します。
キャビテーションの物理モデル構築が困難な最大の理由は、この現象が本質的にマルチスケール現象であるためです。つまり、全く異なる大きさの現象が同時に、そして相互に影響し合いながら進行します。このミクロスケールで発生したマイクロジェットや衝撃波が、プロペラなどの表面を侵食(エロージョン)させ、材料を破壊する直接的な原因となります。マクロな流れのモデルと、ミクロな気泡崩壊のモデルを同時に、かつ正確に計算することは極めて困難です
解析対象・解析手法#
本解析では、NACA0015翼周りの2次元キャビテーション解析についてご紹介します。支配方程式は2次元圧縮性Navier-Stokes方程式です。キャビテーションモデルとして井小萩モデルを用いており、これは相変化量は飽和蒸気圧との圧力差に比例するというモデルです。状態方程式として気液二相状態方程式を使用しています。
解析手法・解析条件を表 1にまとめています。
表 1.解析手法・解析条件
| 項目 | 設定 | 備考 |
|---|---|---|
| 支配方程式 | 2次元圧縮性Navier-Stokes方程式 | |
| 空間離散化 | 3次精度風上差分 | |
| 乱流モデル | RNG k-ε 乱流モデル | RANSでは剥離を良好に予測 |
| 初期状態 | u=8.0[m/s], p=49 [kPa], Y=1.0e-6 | void率~0.3% |
| 流入境界 | u=8.0[m/s], Y=1.0e-10 | |
| 流出境界 | 圧力固定(p=49 [kPa]) | σ=1.4相当 |
| 物性値 | 水(300[K])の物性値を使用 |
計算格子#
解析領域を図 1 に示します。 計算格子は、迎角A.o.A.=8 degのNACA0015翼周りに作成した以下のような格子で、翼弦長をc(=15 [cm])とすると、上流側に4c、下流側に5c、翼上下に2cの領域を確保しています。 節点数 515,850、要素数 342,000です。
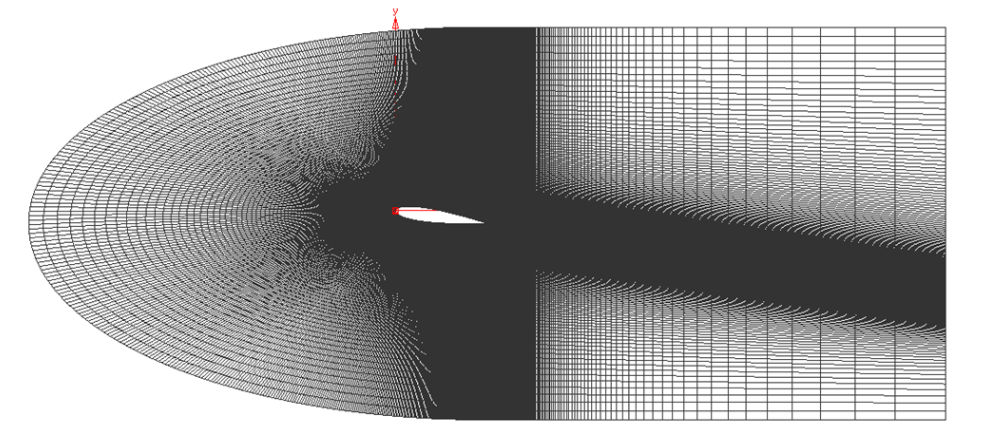
図 1. 解析領域
解析結果#
結果を以下に示します。以下の図2はシートキャビティからクラウドキャビティ放出の様子を表しています。
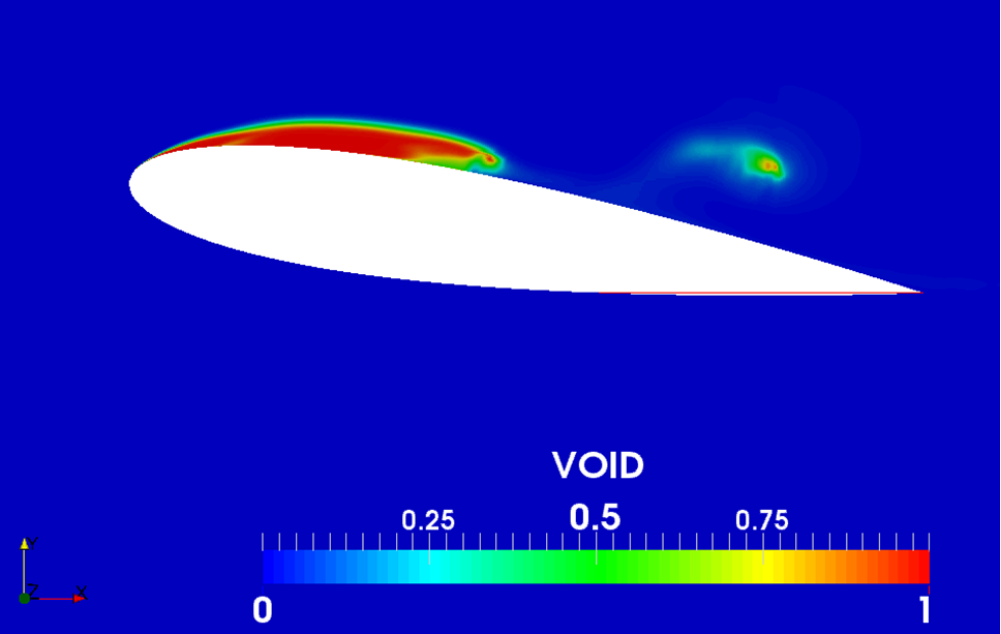
図 2.シートキャビティからクラウドキャビティ放出の様子
以下の図はクラウドキャビティにおけるボイド率放出の変動履歴を表したものです。ここからストローハル数を計算すると、
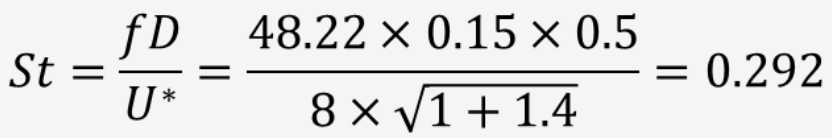
となり、文献値(~0.3)とほぼ一致しました。ここで、Dは最大のシードキャビティ長さであり、U*はキャビティ表面における速度です。
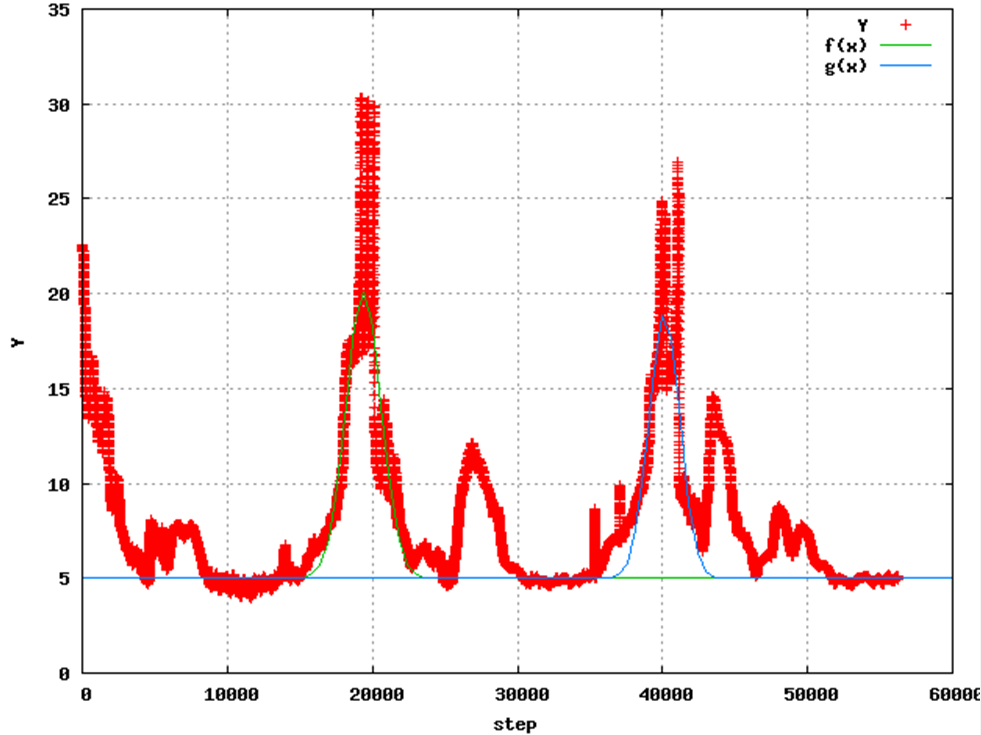
図 3.クラウドキャビティにおけるボイド率の変動
以下の図はボイド率と、それに対応した流速ベクトルの変化を表しており、リエントラントジェットの再現ができていることが確認できました。
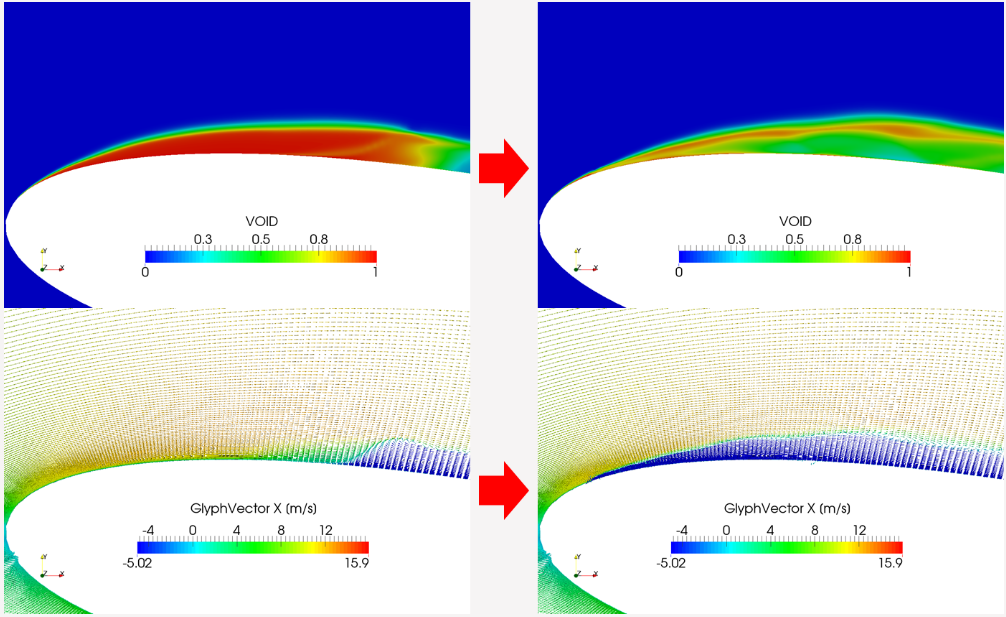
図 4.リエントラントジェットにおける流速ベクトルの変化
以下の図5は、発生したキャビテーション長を示しており、別ソルバーとコンシステントな結果となることが確認できました。
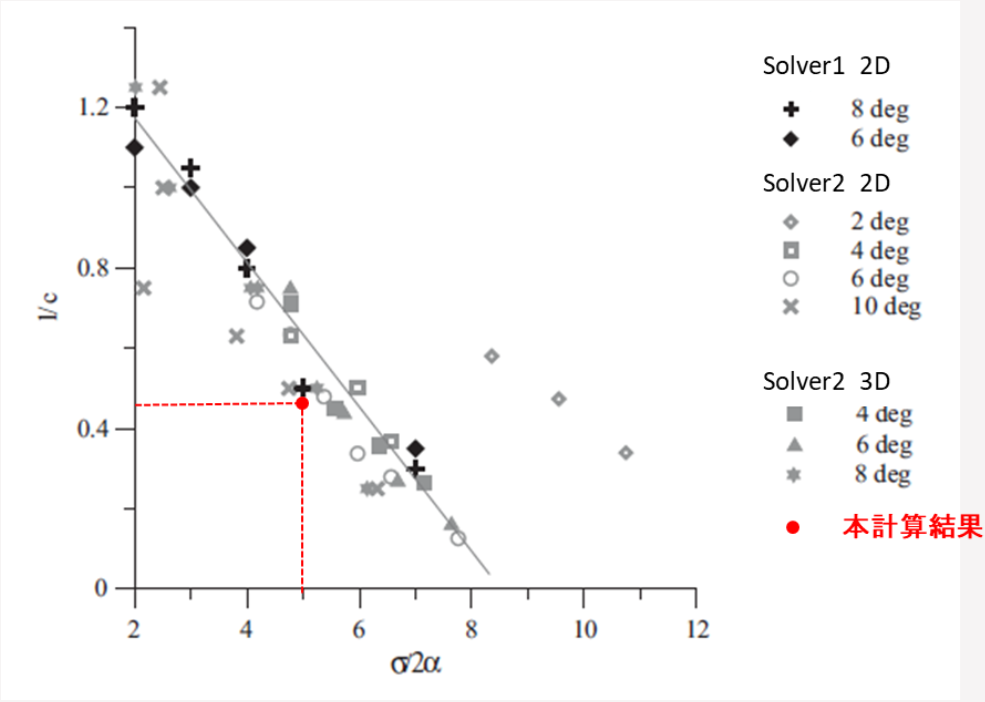
図 5.キャビテーション長の予測
まとめ#
NACA0015(A.o.A.=8deg)翼周り2次元キャビテーション解析を実施しました。解析結果から、シートキャビティの成長、リエントラントジェットの生成、クラウドキャビティの放出という定性的な現象の一部を再現できました。また、キャビテーション長も同じ均質媒体モデルを用いたソルバーと近い結果になっており、使用したモデルの解析結果としては妥当と考えられます。
(*1)参考文献:J. K. Jakobsen, “Supercavitating cascade flow analysis,” Journal of Fluid Engineering, Vol. 86, Issue 4, pp. 805-813, 1964.
(*2)参考文献:鈴木 貴之、加藤 千幸、”均質媒体モデルを用いたキャビテーション解析の問題、” 日本機械学会論文集B編、79巻、808号、pp. 2743-2758、2013.