衝突噴流による沸騰冷却の検証解析#

概要#
Katto and Kunihiro[1]により、水の噴流を高温固体に衝突させ、固体を沸騰冷却する実験で作成した沸騰曲線[2]と比較した解析事例をご紹介します。
参考文献
[1] Katto,Y. and Kunihiro,M.,"Study of the mechanism of burn-out in boiling system of high burn-out heat flux", Bull.JSME,16(1973)1357-1366.
[2] Narumanchi,S.,Troshko,A.,Hassani,V.,Bharathan,D.,"Numerical Simulations of Boiling Jet Impingement Cooling in Power Electronics", Conference Paper NREL/CP-540-39401(2006)1-11.
解析条件#
図1に計算格子と境界条件を示します。Katto and Kunihiroの実験条件を使用し、加熱壁下面を温度固定の境界条件とします。加熱壁下面の温度をパラメータとし、時間進行法による定常解析を行い、表面(固体と流体が接する面)の温度と熱流束を求めます。ただし、固体は銅で熱伝導率が大きく、また厚さが小さいため、加熱壁下面と表面の温度差は小さい結果となります。
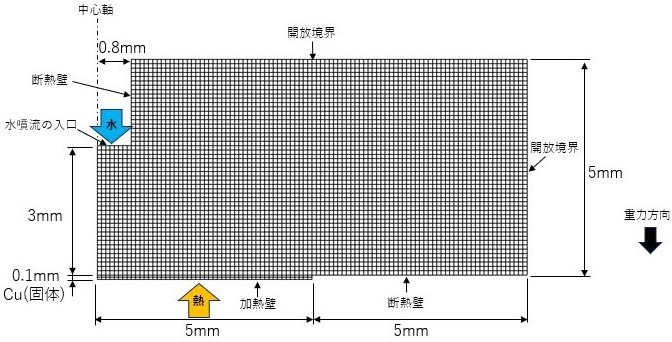
図1 計算格子と境界条件
| 解析条件 | 設定値 |
|---|---|
| 噴流口の半径 | 0.8 mm |
| 流体 | 水と水蒸気 |
| 固体 | 銅 |
| 噴流水の速度 | 2 m/s |
| 噴流水の温度 | 97 ℃ |
| 飽和温度 | 100 ℃ |
| 入熱範囲 | 中心軸から半径5mm |
| 加熱壁下面の温度 | 110, 115, 120, 122.5, 125, 127.5, 130 ℃ |
| 気液二相流の扱い | 二流体モデル |
| 乱流モデル | k-εモデル |
| 重力加速度 | 9.80665 m/s2 |
| 次元 | 2次元軸対称 |
| 半径方向の格子数 | 100(中心軸から開放境界まで) |
| 軸方向の格子数 | 52(加熱壁から開放境界まで) |
| 時間刻み | 10-5 s |
| 計算する現象時間 | 4 s |
解析結果#
加熱壁下面の温度を変えた全てのケースについて、現象時間1sで準定常状態に達しました。1sから4sまでを時間平均した結果を以下に示します。
中心軸上の固体表面における沸騰曲線を図3に示します。赤色のプロットはKatto and Kunihiroの実験結果で、青色のプロットは計算結果です。計算結果は実験結果と概ね一致しています。
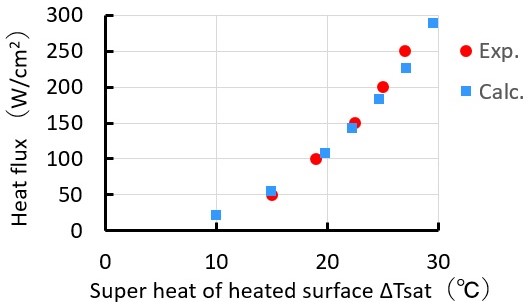
図3 衝突噴流における沸騰曲線
熱流束 250 W/cm2 の計算結果について、ボイド率分布、水の速度分布、水蒸気の速度分布を以下に示します。
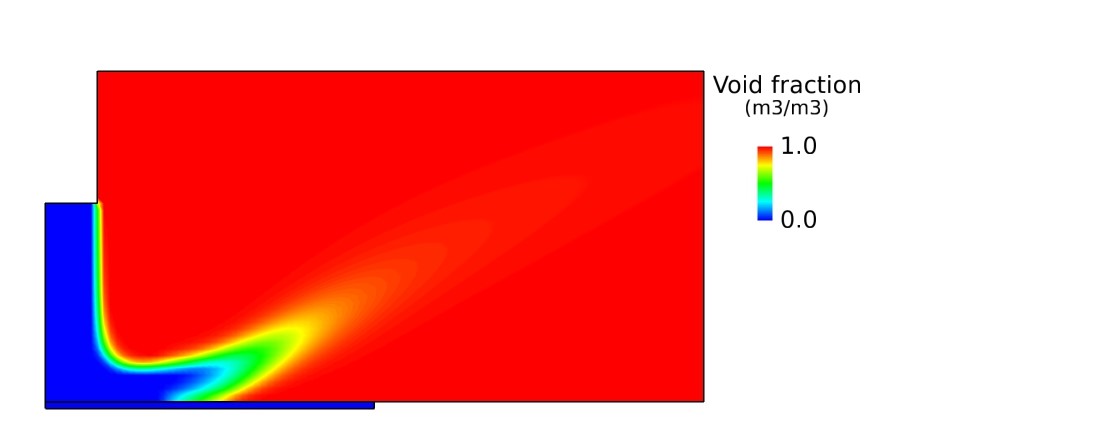
図4 ボイド率分布
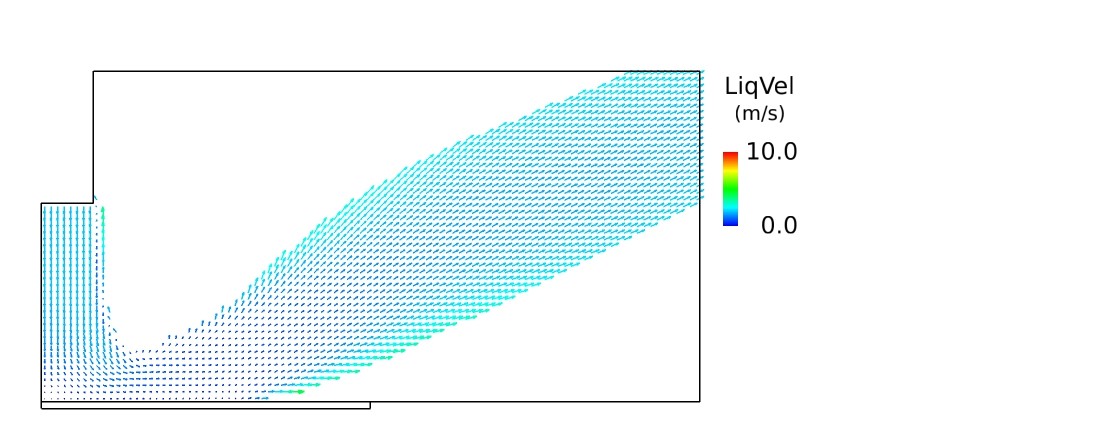
図5 水の速度分布
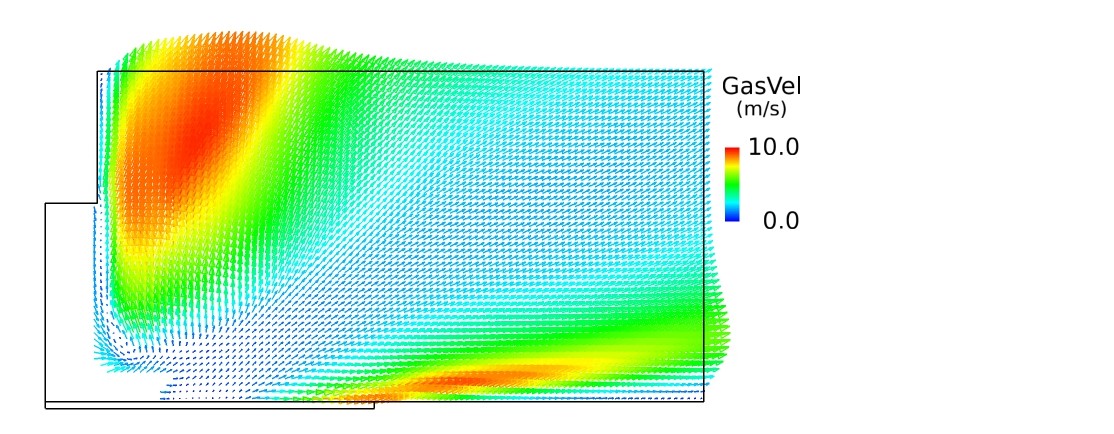
図6 水蒸気の速度分布
本解析でわかったこと#
衝突噴流による沸騰冷却において、Katto and Kunihiroの実験による沸騰曲線を概ね再現できることがわかりました。
関連ページ#
- 気液二相流解析ソフトウェア Advance/FrontFlow/MP
- 解析分野:流体
- 産業分野:産業機械
- 産業分野:材料・化学
- 産業分野:原子力