空気と水蒸気の混合気体の凝縮解析#

概要#
空気と水蒸気の混合気体が鉛直壁面で凝縮する強制対流の解析事例をご紹介します。Dehbi[1]による空気と水蒸気の混合気体に対する壁面凝縮熱伝達率の実験相関式(1)とバルクの計算値を使用することで、壁面付近のメッシュサイズを大きくしています。また、一般的に凝縮熱伝達率は強制対流熱伝達率より大きいため、Dehbiの式を強制対流の計算に使用しています。
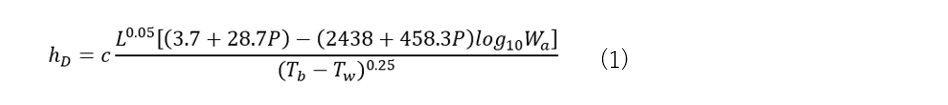
ここで、cは平面壁では1、曲面壁では1.25、Lは凝縮面の長さ、Pは絶対圧[bar]、Waはバルクの空気質量分率、Tbはバルクの温度、Twは壁面温度です。
[1]A.Dehbi,"Correcting for tube curvature effects on condensation in the presence of a noncondensable gas in turbulent free convection",Int.J.Heat Mass Transf.164(2021)1-11.
解析条件#
図1に計算格子と境界条件を示します。空気と水蒸気と水の物性値は1atm、100℃の値を使用しました。
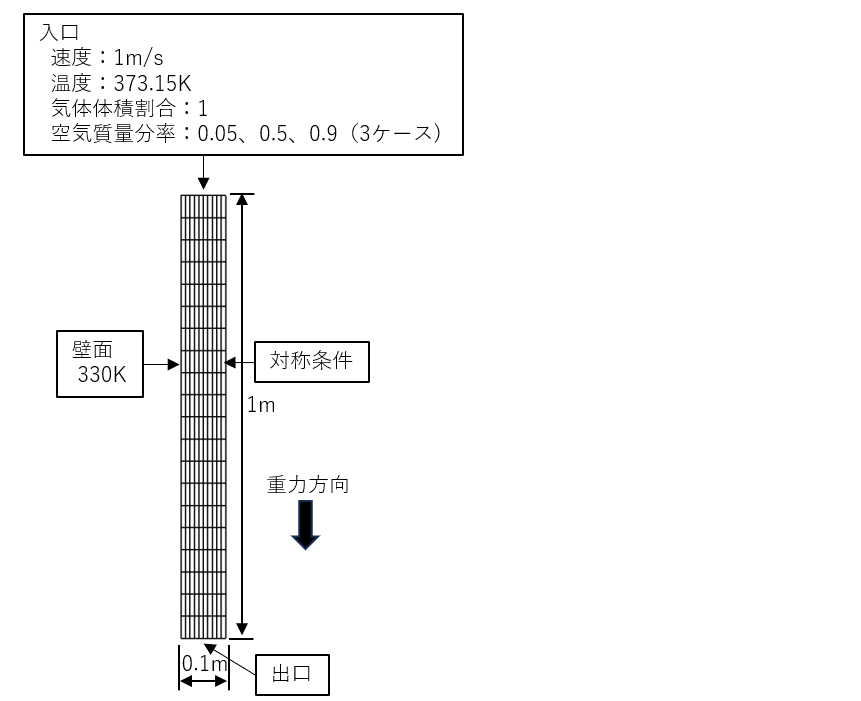
図1 計算格子と境界条件
| 解析条件 | 設定値 |
|---|---|
| 次元 | 2 |
| 解析領域 | 1 m(鉛直方向) × 0.1 m(水平方向) |
| 空気の密度 | 0.9458 kg/m3 |
| 空気の粘性係数 | 2.181x10-5 Pa・s |
| 空気の熱伝導率 | 3.129x10-2 W/(m・K) |
| 水蒸気の密度 | 0.5982 kg/m3 |
| 水蒸気の粘性係数 | 1.223x10-5 Pa・s |
| 水蒸気の熱伝導率 | 2.457x10-2 W/(m・K) |
| 水蒸気の飽和エンタルピ | 2.676x106 J/kg |
| 水の密度 | 958.4 kg/m3 |
| 水の粘性係数 | 2.816x10-4 Pa・s |
| 水の熱伝導率 | 6.772x10-1 W/(m・K) |
| 水の飽和エンタルピ | 4.192x105 J/kg |
| 飽和温度 | 373.15 K |
| 入口の速度 | 1 m/s |
| 入口の温度 | 373.15 K |
| 入口の気相体積割合 | 1 |
| 入口の空気質量分率 | 0.05, 0.5, 0.9 (3ケース) |
| 壁面温度 | 330 K |
| 凝縮面の長さ | 1 m |
| 壁面からバルクまでの距離 | 0.05 m |
| 水平方向の格子数 | 10(等分割) |
| 水平方向のメッシュサイズ | 0.01 m |
| 垂直方向の格子数 | 20(等分割) |
| 垂直方向のメッシュサイズ | 0.05 m |
| 時間刻み | 10-3 s |
解析結果#
平均凝縮質量流束の計算結果とDehbiの実験結果を図2に示します。計算は実験相関式を使用しているため、計算結果はDehbiの実験曲線上にあります。
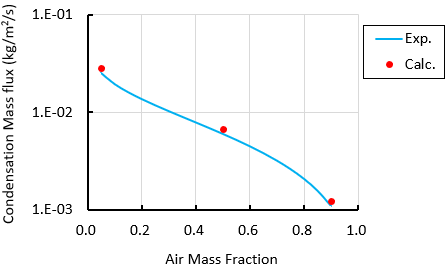
図2 平均凝縮質量流束
水蒸気質量分率の計算結果を図3に示します。各ケースのカラーバーの範囲は計算結果の最小値から最大値までとしています。
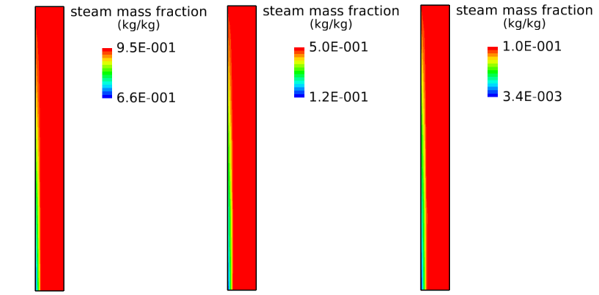
Wa=0.05 Wa=0.5 Wa=0.9
図3 水蒸気質量分率(Waは入口空気質量分率)
気相密度の計算結果を図4に示します。各ケースのカラーバーの範囲は計算結果の最小値から最大値までとしています。
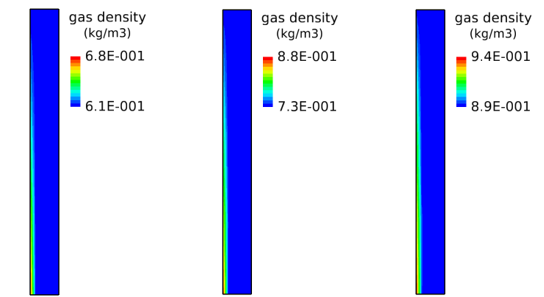
Wa=0.05 Wa=0.5 Wa=0.9
図4 気相密度(Waは入口空気質量分率)
液相体積割合の計算結果を図5に示します。各ケースのカラーバーの範囲は計算結果の最小値から最大値までとしています。入口空気質量分率が小さいほど(=入口水蒸気質量分率が大きいほど)壁面凝縮熱伝達率が大きいため、壁面上の液相体積割合が大きい結果となっています。
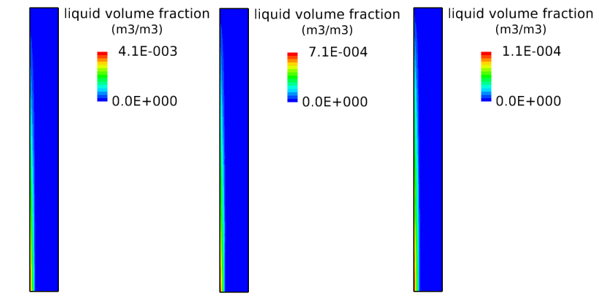
Wa=0.05 Wa=0.5 Wa=0.9
図5 液相体積割合(Waは入口空気質量分率)
本解析でわかったこと#
Dehbiによる空気と水蒸気の混合気体に対する壁面凝縮熱伝達率の実験相関式とバルクの計算値を使用することで、壁面付近のメッシュサイズを大きくして、空気と水蒸気の混合気体が鉛直壁面で凝縮する計算ができることを確認しました。 本ソフトウェアには場所毎に壁面からバルクまでの距離を変える機能が実装されていますが、複雑な3次元流動計算を行う場合にこの距離をどのように与えるかが課題となります。
関連ページ#
- 気液二相流解析ソフトウェア Advance/FrontFlow/MP
- 解析分野:流体
- 産業分野:産業機械
- 産業分野:原子力