コンテンツにスキップ

URANS(k-ω SST)とSST-DDESによる円柱周りのレイノルズ数効果の検証解析#

解析対象#

種々のレイノルズ数での円柱周りの層流 / 乱流剥離を伴う非定常現象

背景#

  1. RANS は定常（Steady）RANS と非定常（Unsteady）RANS（URANS）に分類される。
  2. URANS では、格子解像度が十分あっても高レイノルズ数における乱流の高周波成分の再現は困難である。
  3. 乱流モデルにおける乱流特性長さ以下の空間変動成分がアンサンブル平均の中に埋没するためである。
  4. Advance/FOCUS-i に実装した DES1 または DDES2 では格子スケールと乱流特性長さを常に比較し、空間平均モデルとして解かれる領域と RANS モデルで解かれる領域を分けるアルゴリズムであり、高いレイノルズ数での非定常乱流挙動と平均的特性の両方に対して高い予測精度が期待できる。
  5. 円柱周りの抗力係数について k-ω SST モデルと SST-DDES モデルの精度を検証した事例を示す。

解析モデル#

  1. RANS モデルは k-ω SST モデルを使用した
  2. SST-DDES は k-ω SST モデルの k の方程式における Destruction 項を修正した乱流モデルを用いた
  3. 流体解析に用いた計算格子は円柱周りに 128 点、奥行き方向に 64 点、壁面から遠方方向に 128 点の要素数で構成される 6 面体格子とした
  4. 奥行方向の計算領域は円柱の直径 D の 4 倍とした
  5. 円柱の中心から遠方境界までの距離は円柱の直径 D の 20 倍とした
  6. 壁面から第 1 格子点までの最小格子幅 Δη は、Re = 100 と Re = 200 の場合は Δη/D = 0.002 とし、 Re = 10,000 の場合は Δη/D = 0.001 とし、その他は Δη/D = 0.00001 とした

解析結果#

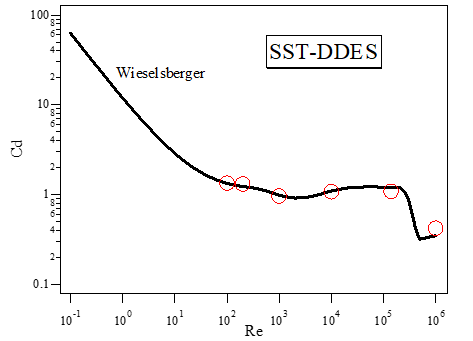
① レイノルズ数は Re = 100、 200、 1,000、 10,000、 140,000、 1,000,000 の 6 ケース

② Re = 100、 200 は渦粘性がほぼ 0 で層流剥離とカルマン渦放出が特徴的な流れ場である

③ Re = 140,000 の場合は層流剥離を起こし、乱流付着する、いわゆる臨界レイノルズ数の状態であり、レイノルズ数が上がるにつれて抗力係数 Cd が若干増加する

④ Re = 1,000,000 以降では乱流剥離をし、剥離渦は速やかに小渦に変化しながら大規模スケールの渦列も構成するという特徴を有し、乱流境界層の存在のために剥離点が円柱の最大投影面よりも後方で生じ、抗力が急減少する、いわゆる drag crisis の領域を再現することを確認した

⑤ SST-DDES モデルはこれらの全てを網羅的に解くことが可能であり、抗力係数は実験3と良く一致するのが見てとれる

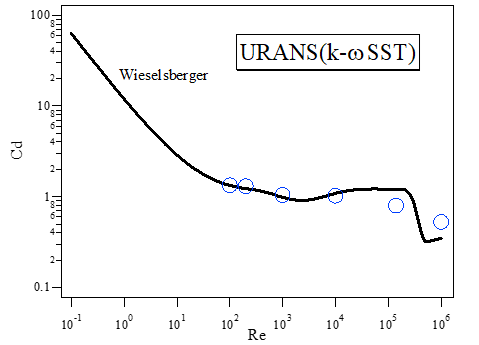
① URANS の結果は、特にレイノルズ数が Re = 140,000 以降の drag crisis 前後から予測精度が低下する

② その Re 数以降では、乱流モデルにおける乱流特性長さ以下の空間変動成分がアンサンブル平均の中に埋没しやすく、一般に言われている通り、URANS の非定常乱流解析に関する脆弱性が現れている。

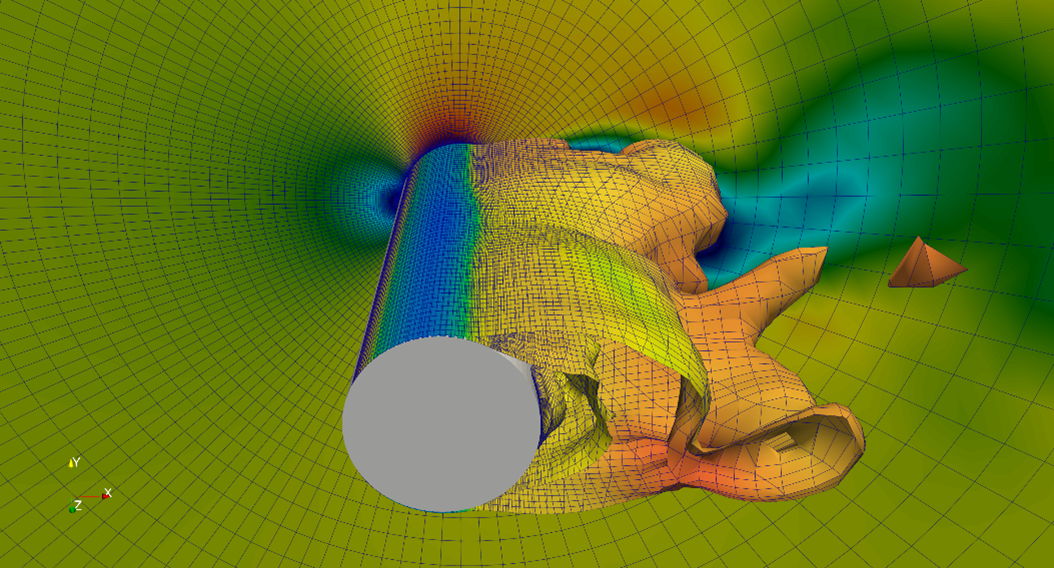
① SST-DDES モデルによる、Re = 1,000,000 の流れのスナップショット

② ｚ = 0 平面での速度の絶対値の可視化

③ 乱流エネルギーの等値面に圧力でカラーリング処理したものを重ね合わせて 3 次元性を可視化

関連ページ#

  1. Spalart, P. R., Jou, W. H., Strelets, M., and Allmaras, S. R., “Comments of the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach,” Advances in DNS/LES, 1st AFOSR Int. Conf. on DNS/LES, (1997) ↩

  2. Spalart, P. R., Deek, S., Shur, M. L., Squires, K. D., Strelets, M., and Travin, A., “A new version of detached-eddy simulation, resistant to ambiguous grid densities,” Theor. Comput. Fluid Dynamics, 20 (2006) pp. 181-195. ↩

  3. Wieselsberger, C., "Neure festellungen uber die gesetze des flussigkeits- und luftwiderstands," Phys, Z., 22 (1921) pp. 321-328 ↩