コンテンツにスキップ

サーマルキャビティ解析#

  • 自然対流解析、熱伝導解析の標準問題

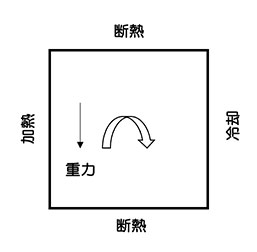
  • 加熱面と冷却面に挟まった正方形内の自然対流解析

  • 最も著名なベンチマーク解 [1] と比較

  • 計算は次のケースを実施

   加熱面 : 温度 280K

   冷却面 : 温度 270K

   X=1.0m 、格子分割数 : 100×100

   完全理想気体、比熱比 1.4

   Prandtl 数 0.71、Rayleigh 数 1,000

   重力加速度 9.80665 [m/s2]



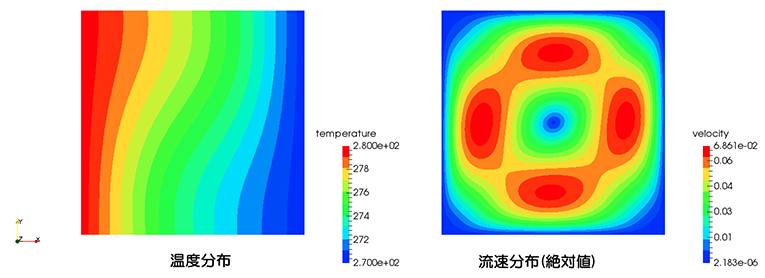
NO. 項目 本計算[注1] ベンチマーク解[注2] 備考
1 平均 Nusselt 数 1.140
（+1.97%）		 1.118 加熱面と冷却面の温度差で無次元化した温度勾配を加熱面に沿って積分
2 水平方向最大流速 3.608
（-1.12%）		 3.649 最大流速は高さと温度拡散係数(熱伝導度と熱容量の比)で流速を無次元化
3 垂直方向最大流速 3.683
（-0.38%）		 3.697 最大流速は高さと温度拡散係数(熱伝導度と熱容量の比)で流速を無次元化


エネルギー保存式とガス濃度質量保存式に対して同一条件とした解析

Ra=1,000 となるように、密度、粘性係数、熱伝導度、拡散係数を与えました。

加熱面：温度1.0K、質量分率：1.0

冷却面：温度0.0K、質量分率：0.0

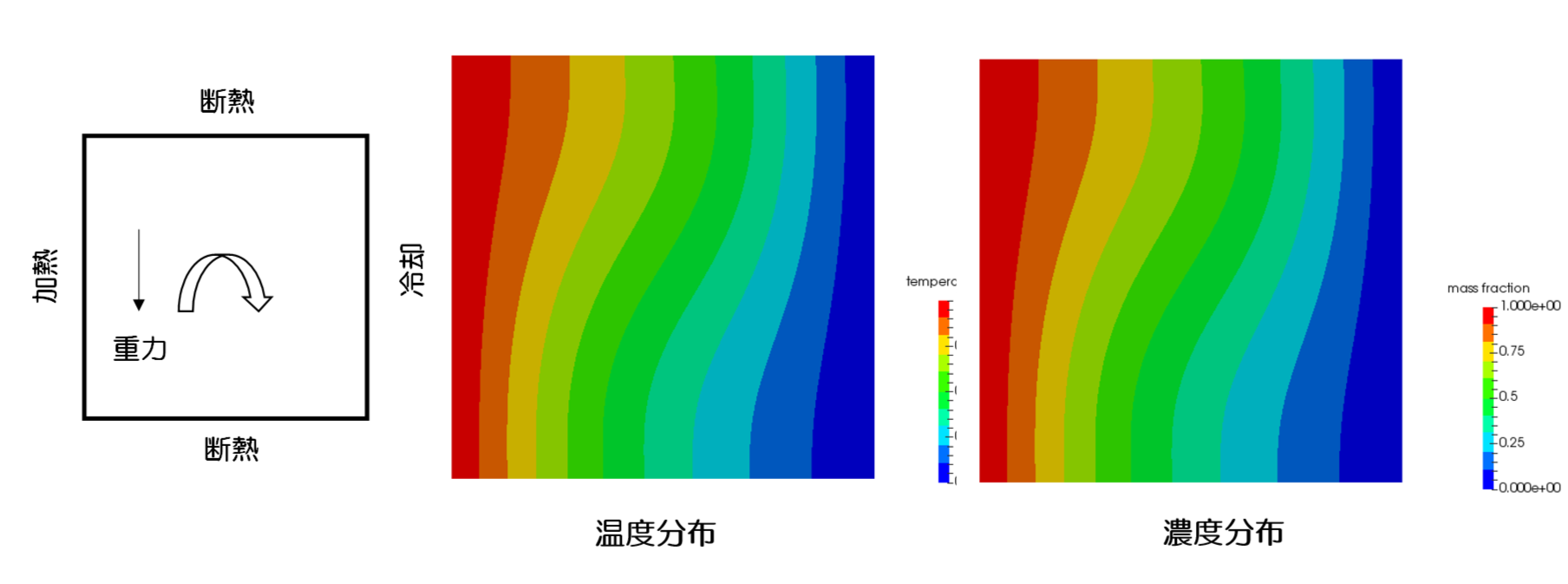
分子量がほぼ等しい 2 成分の解析

窒素と一酸化炭素の 2 成分、Ra=1,000 となるように輸送係数を 1,000 倍としました。

加熱面：温度280.0K、質量分率：窒素0.0、一酸化炭素1.0

冷却面：温度270.0K、質量分率：窒素1.0、一酸化炭素0.0

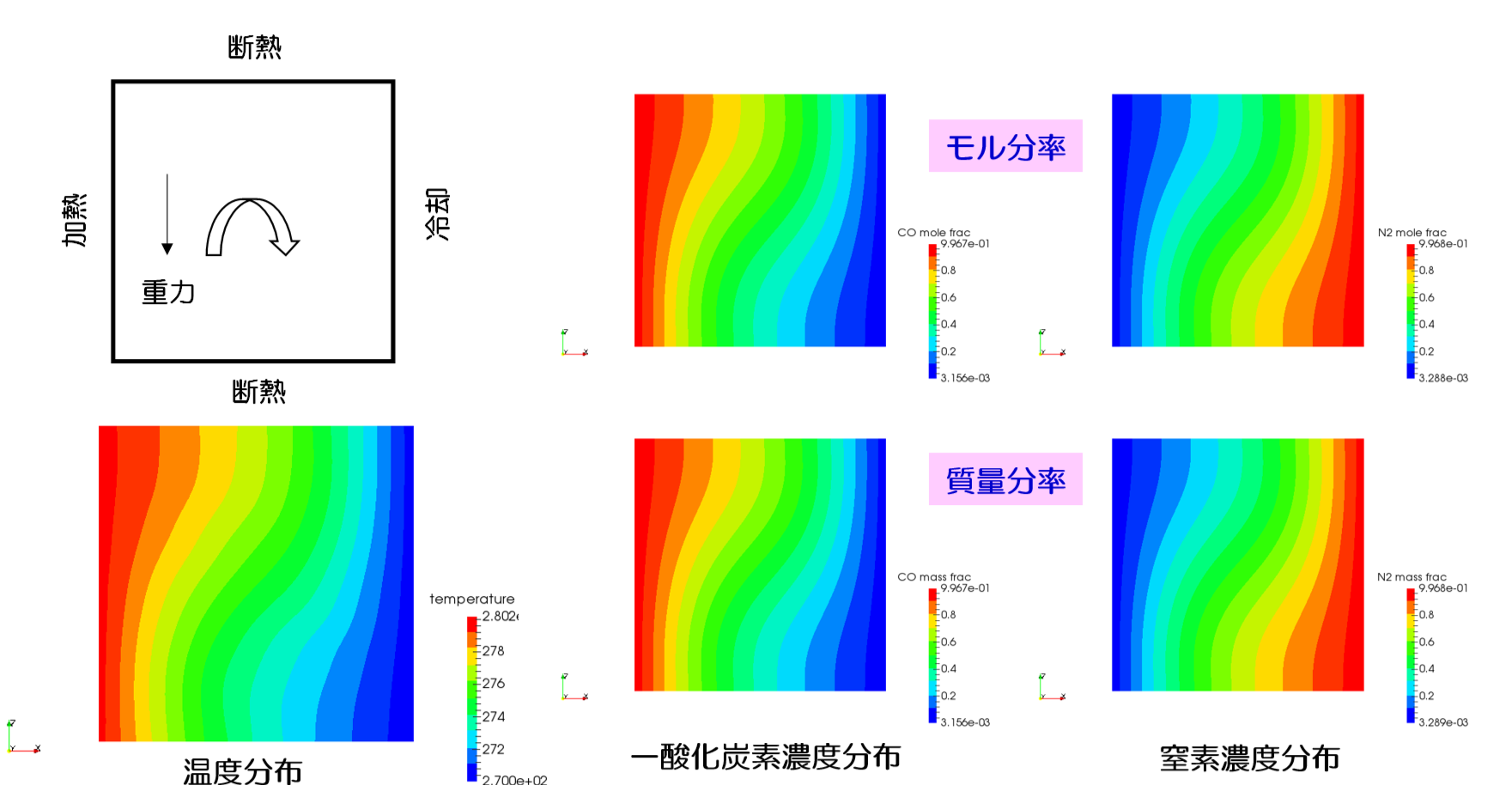
備考#

[1] de Vahl Davis, G., “Natural convection of air in a square cavity: A benchmark numerical solution”, Int. J. Numer. Methods Fluids, 3 (1983) 249-254.

[注1] カッコ内の数値はベンチマーク解との差異

[注2] de Vahl Davis, G., “Natural convection of air in a square cavity: A benchmark numerical solution”, Int. J. Numer. Methods Fluids, 3 (1983) 249-254.

関連ページ#